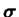 |
tenseur des contraintes de Cauchy (d'ordre
2) |
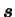 |
tenseur des contraintes déviatoires (d'ordre
2) (
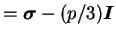 ) ) |
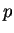 |
contrainte isotrope ou sphérique |
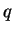 |
contrainte équivalent de Von Mises |
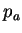 |
pression atmosphérique |
|
|
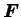 |
tenseur du gradient des transformations (d'ordre 2) |
 |
tenseur du gradient des taux de transformations (d'ordre 2) |
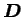 |
tenseur du gradient des taux de déformations (d'ordre 2) |
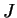 |
jacobien des transformations |
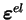 |
tenseur des déformations
élastiques (d'ordre 2) |
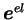 |
tenseur des déformations élastiques
déviatoires (d'ordre 2) |
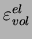 |
déformation volumique élastique |
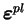 |
tenseur des déformations
plastiques (d'ordre 2) |
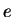 |
indice des vides |
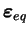 |
tenseur des déformations
équivalentes |
|
|
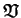 |
volume spécifique |
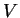 |
volume total |
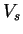 |
volume de la partie solide (squelette) |
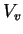 |
volume des vides |
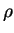 |
masse volumique |
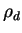 |
masse volumique du matériau dense |
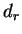 |
densité relative à la masse volumique de l'eau |
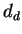 |
densité relative à la masse volumique du matériau dense |
|
|
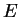 |
module d'Young |
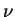 |
coefficient de Poisson |
 |
module de cisaillement |
 |
module d'élasticité volumique |
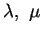 |
coefficients de Lamé |
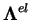 |
matrice d'élasticité |
 |
multiplicateur plastique |
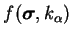 |
surface de charge ou limite
d'élasticité |
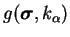 |
potentiel plastique |
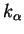 |
paramètres d'écrouissage |
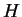 |
module d'écrouissage |
|
|
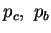 |
pression isotrope de consolidation |
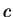 |
cohésion isotrope |
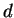 |
cohésion déviatoire |
 |
angle de frottement interne |
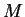 |
pente de la droite d'état critique |
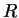 |
excentricité du Cap |
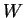 |
potentiel |
|
|
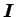 |
tenseur identité d'ordre 2 |
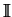 |
matrice identité d'ordre 4 |
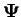 |
fonction tensorielle |
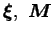 |
tenseurs de structures |
|
|
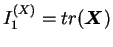 |
premier invariant du tenseur
 |
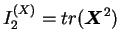 |
deuxième invariant du tenseur
 |
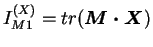 |
premier invariant
du tenseur
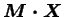 |
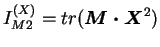 |
deuxième
invariant du tenseur
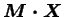 |
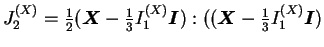 |
deuxième invariant du tenseur
 |
|
|