



suivant: Théorie plastique pour les
monter: Modèles plastiques anisotropes
précédent: Modèles plastiques anisotropes
Table des matières
La théorie simplifiée des fonctions
tensorielles
Le but de cette théorie est de mettre en relief l'anisotropie
d'une manière simple et de pouvoir traiter le milieu avec les
techniques mises au point dans le cas isotrope. Boehler [BOE75]
introduit un tenseur transformé
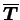 défini
par :
défini
par :
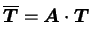 |
(4.29.1) |
où
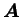 est un tenseur du quatrième ordre dont les
composantes représentent certains coefficients d'anisotropie du
milieu. Ce tenseur vérifie les symétries suivantes :
Considérons une relation linéaire isotrope entre les tenseurs
est un tenseur du quatrième ordre dont les
composantes représentent certains coefficients d'anisotropie du
milieu. Ce tenseur vérifie les symétries suivantes :
Considérons une relation linéaire isotrope entre les tenseurs
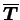 et
et
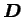 :
:
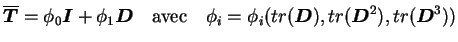 |
(4.29.2) |
Cette équation (4.5.2) combinée à la condition
d'homogénéité de degré zéro par rapport au
temps4.1 permet4.2 d'obtenir le critère suivant :
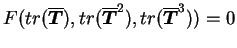 |
(4.29.3) |
La forme du critère donnée dans l'équation 4.5.3 est
isotrope dans cet espace transformé. La transformation inverse
pour revenir à l'espace initial donne alors un critère anisotrope.
Ainsi, il est possible d'établir un critère de plasticité
anisotrope à partir d'une relation isotrope.




suivant: Théorie plastique pour les
monter: Modèles plastiques anisotropes
précédent: Modèles plastiques anisotropes
Table des matières
FRACHON Arnaud
2002-11-12