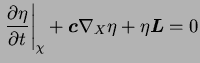suivant: Interactions entre surfaces
monter: Le code éléments finis
précédent: Abaqus/Explicit
Table des matières
Maillage adaptatif
Le but de cet outil est d'assurer une grande qualité au maillage
au cours de la simulation numérique lorsque de grandes
déformations sont appliquées. La réalisation ne consiste pas en
une modification des éléments finis et de leurs dispositions (ni
création ni destruction d'élément). La technique combine une
analyse Lagrangienne et une analyse Eulérienne. Le terme consacré
est "ALE" (Arbitrary Lagrangian-Eulerian).
L'évolution de la densité relative 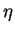 est donnée par le
principe de conservation de la masse, dont la description ALE
formule :
est donnée par le
principe de conservation de la masse, dont la description ALE
formule :
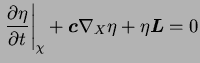 |
(5.33.1) |
où 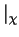 signifie à maillage fixe,
signifie à maillage fixe,
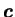 est
la vitesse convective et
est
la vitesse convective et
 est tenseur gradient des
vitesses. La vitesse de convection se définit par la différence
entre la vitesse de la matière et la vitesse du maillage. Si cette
vitesse convective est nulle, la description est Lagrangienne. Par
contre, si
est tenseur gradient des
vitesses. La vitesse de convection se définit par la différence
entre la vitesse de la matière et la vitesse du maillage. Si cette
vitesse convective est nulle, la description est Lagrangienne. Par
contre, si
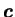 correspond à la vitesse de la matière
(le maillage est immobile), la description est Eulérienne
[MAË93].
La description ALE permet ainsi d'avoir un écoulement de la
matière au travers du maillage tout en entraînant celui-ci. Cette
description peut ainsi répartir les déformations volumiques et les
distorsions dans respectivement la description Lagrangienne et la
description Eulérienne. Ainsi, le maillage n'est pas soumis à des
distorsions excessives. Ces dernières sont à l'origine de
non-convergences pour les simulations numériques avec abaqus/explicit.
correspond à la vitesse de la matière
(le maillage est immobile), la description est Eulérienne
[MAË93].
La description ALE permet ainsi d'avoir un écoulement de la
matière au travers du maillage tout en entraînant celui-ci. Cette
description peut ainsi répartir les déformations volumiques et les
distorsions dans respectivement la description Lagrangienne et la
description Eulérienne. Ainsi, le maillage n'est pas soumis à des
distorsions excessives. Ces dernières sont à l'origine de
non-convergences pour les simulations numériques avec abaqus/explicit.




suivant: Interactions entre surfaces
monter: Le code éléments finis
précédent: Abaqus/Explicit
Table des matières
FRACHON Arnaud
2002-11-12