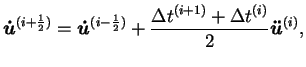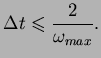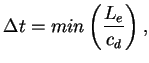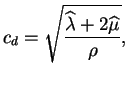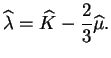suivant: Maillage adaptatif
monter: Schémas explicite
précédent: Principe général
Table des matières
La version explicite est entièrement vectorisée afin d'utiliser
les supercalculateurs multiprocesseurs.
Bien que l'analyse soit dynamique, elle peut être utilisée
moyennant quelques précautions (voir 5.6) pour accomplir
des analyses quasi-statiques. Le schéma explicite implanté au sein
du Abaqus conduit à des temps de calcul plus faibles
comparativement au schéma implicite nommé Abaqus/Standard.
L'algorithme explicite assure une certaine robustesse, il est plus
efficace pour aboutir à un calcul complet que Abaqus/Standard. Ce
code présente une bonne résolution des contacts ce qui est un
autre intérêt vis-à-vis de la simulation du procédé.
ABAQUS/Explicit met en  uvre un schéma d'intégration par
différences centrales exprimé par les équations (5.2.5) et
(5.2.6).
uvre un schéma d'intégration par
différences centrales exprimé par les équations (5.2.5) et
(5.2.6).
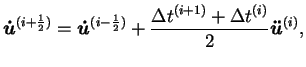 |
(5.32.5) |
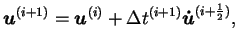 |
(5.32.6) |
où
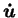 est la vitesse et
est la vitesse et
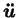 est l'accélération. L'exposant
est l'accélération. L'exposant 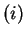 indique le numéro de l'incrément. Ces équations sont illustrées
sur la figure 5.2.4.
indique le numéro de l'incrément. Ces équations sont illustrées
sur la figure 5.2.4.
Figure 5.2.4:
Illustration de l'opérateur de différence centrale
|
|
Ce seul schéma d'intégration est combiné à une procédure
dynamique. La clef de l'efficacité calculatoire de la procédure
explicite provient de l'utilisation d'une matrice de masse
diagonale. Une telle forme permet un calcul rapide de l'inverse de
cette matrice notamment utilisée pour la détermination de
l'accélération de l'équation (5.2.7).
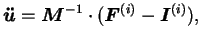 |
(5.32.7) |
où
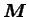 est la matrice de masse diagonale,
est la matrice de masse diagonale,
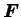 est le vecteur des charges appliquées et
est le vecteur des charges appliquées et
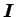 est le
vecteur des forces internes. Ainsi, la procédure explicite ne
requiert ni itération ni matrice tangente de rigidité.
La procédure explicite intègre par rapport au temps en utilisant
beaucoup de petits incréments de temps. Or, l'opérateur de
différences centrales est conditionnellement stable. La limite de
cette stabilité pour cet opérateur est donnée en terme de plus
grande valeur propre du système par
Une estimation de la plus petite valeur propre du système peut
être obtenue en déterminant le mode maximum des éléments du
maillage. Ainsi, l'incrément de temps permettant la stabilité est
donnée par
où
est le
vecteur des forces internes. Ainsi, la procédure explicite ne
requiert ni itération ni matrice tangente de rigidité.
La procédure explicite intègre par rapport au temps en utilisant
beaucoup de petits incréments de temps. Or, l'opérateur de
différences centrales est conditionnellement stable. La limite de
cette stabilité pour cet opérateur est donnée en terme de plus
grande valeur propre du système par
Une estimation de la plus petite valeur propre du système peut
être obtenue en déterminant le mode maximum des éléments du
maillage. Ainsi, l'incrément de temps permettant la stabilité est
donnée par
où 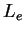 est la dimension caractéristique des éléments et
est la dimension caractéristique des éléments et 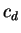 est la vitesse des ondes en dilatation dans le matériau. Cette
vitesse est donnée par
avec
Le tenseur
est la vitesse des ondes en dilatation dans le matériau. Cette
vitesse est donnée par
avec
Le tenseur
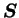 est le tenseur des contraintes
déviatoires et
est le tenseur des contraintes
déviatoires et
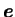 est le tenseur des déformations
déviatoires.
est le tenseur des déformations
déviatoires. 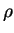 est la masse volumique du matériau.
Ainsi, la procédure explicite dynamique peut effectuer un grand
nombre de petits incréments pour un temps de calcul raisonnable.
est la masse volumique du matériau.
Ainsi, la procédure explicite dynamique peut effectuer un grand
nombre de petits incréments pour un temps de calcul raisonnable.




suivant: Maillage adaptatif
monter: Schémas explicite
précédent: Principe général
Table des matières
FRACHON Arnaud
2002-11-12