Mise en uvre des modèles éléments finis

Cette section est dédiée aux aspects propres à la mise en pratique du code pour la simulation du procédé. Les résultats issus de cette pratique seront exposés au chapitre suivant. Les maillages sont construits à partir d'un type d'éléments finis nommé CAX4R. Il s'agit d'éléments rectangulaires à 4 nuds prenant en compte la symétrie cylindrique (AX). Ces éléments possèdent un unique point de Gauss (R). Cette dernière caractéristique du type CAX4R pourrait entraîner des effets artificiels sur le mode de déformation du maillage associé au matériaux soumis à des chargements mécaniques. En effet, il est possible d'obtenir des déformations des éléments à volume constant de façon artificielle (non-lié à un phénomène physique) et ce propager rapidement à l'ensemble du maillage. La projection en un unique point de Gauss ne permet pas de rendre compte de la forme de l'élément. Pour éviter cette possibilité, ces éléments sont munis d'une fonction de contrôle de l'effet "sablier" (hourglass control). Cette fonction engendre une énergie qui n'est pas prise en compte dans le bilan énergétique.

Figure 5.6.1: Effet sablier : les éléments se déforment à volume constant

La forme des pièces, la cinématique des poinçons et l'effet du frottement sont autant d'aspects qui gênèrent des champs de contraintes et de déformations hétérogènes au sein du massif de poudre. Ainsi, la densité de maillage doit être fonction des gradient des grandeurs physique à simulées. Par ailleurs, il convient par une procédure d'augmentation systématique du nombre d'éléments d'identifier le nombre minimum d'éléments qui stabilise les résultats numériques. Le nombre de nuds et leurs répartitions sont le résultats de divers essais de maillage. Ainsi il est obtenu un maillage qui tient compte de la cinématique des outils et de la compression des éléments. Les différents maillages utilisés pour les calculs seront présentés dans le chapitre suivant. Comme cela a été signalé à la section 5.2.2, le schéma de résolution explicite a pour avantages une robustesse numérique, des temps de calculs raisonnables (par rapport au nombre d'opérations effectuées) et une bonne précision dans la gestion des contacts. La mise en uvre de ce schéma essentiellement dédiée aux simulations de problèmes dynamiques nécessitent quelques précautions pour le traitement de cas quasi-statique. La plus importante est de maîtriser l'inertie du problème considéré de sorte que ce phénomène puisse être minimisé. Dans le cas de la compression à froid, l'énergie est apportée de l'extérieur par les poinçons sous forme de déplacement pour induire des déformations. Ainsi, le contrôle des phénomènes inertiels est effectué au travers de la comparaison entre l'énergie cinétique et l'énergie de déformation. Afin de réduire les temps de calculs, soit l'analyse est réduite, soit on augmente la masse du modèle artificiellement. L'augmentation de la masse du modèle induit un accroissement du plus petit incrément de temps stable ($\Delta t$). 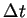Cette augmentation est obtenue par une factorisation de la masse conduisant à une réduction significative du temps de calculs (jusqu'à dix fois plus rapide). Cependant, cette outil est à manipuler avec précaution car les effets qu'il induit peuvent altérer significativement la solution de la simulation. L'ensemble de ces remarques est recommandations sont mises en uvres dans les chapitres suivant. L'objectif étant d'obtenir des simulations numériques les plus fiables possibles en un minimum de temps de calcul.