suivant: Abaqus/Explicit
monter: Schémas explicite
précédent: Schémas explicite
Table des matières
Le principe de ce schéma est de résoudre l'équation d'équilibre
pour l'instant
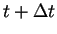 à partir des données de l'instant
à partir des données de l'instant
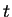 . Ce schéma permet de déterminer les variables nodales
. Ce schéma permet de déterminer les variables nodales
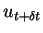 en fonction de leurs valeurs en début d'incrément de
temps
en fonction de leurs valeurs en début d'incrément de
temps 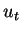 .
.
Figure 5.2.3:
Illustration du schéma explicite d'intégration au cours
du temps
|
|
La figure 5.2.3 illustre la méthode des différences
finies explicites où la solution à l'instant
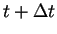 n'est
fonction que des valeurs nodales et de ces dérivées à l'instant
n'est
fonction que des valeurs nodales et de ces dérivées à l'instant
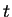 comme l'indique le système suivant.
Cette méthode de résolution ne peut admettre des incréments de
temps trop importants sous peine de divergences des calculs. La
convergence n'est assurée que si l'incrément de temps
comme l'indique le système suivant.
Cette méthode de résolution ne peut admettre des incréments de
temps trop importants sous peine de divergences des calculs. La
convergence n'est assurée que si l'incrément de temps 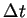 est inférieur à un incrément critique
est inférieur à un incrément critique
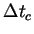 .
.
FRACHON Arnaud
2002-11-12