



suivant: Étude de sensibilité
monter: Pièces de validation
précédent: Résultats des simulations
Table des matières
Ce chapitre présente des résultats de simulation numérique du
procédé de compression en matrices. Ces simulations portent sur
deux pièces industrielles pour lesquelles le procédé a été
modélisé de différentes façons. Les résultats de ces simulations
ont été comparés aux mesures expérimentales disponibles pour
chaque type de pièce.
Des approximations sont faites lors de la définition des modèles
élément finis. Le coefficient de frottement est supposé constant
pour une valeur de 0.1. Ce coefficient évolue en fait au cours de
la compression car il est lié à la valeur de la masse volumique.
Dans le cas de la poudre Distaloy AE, le coefficient de frottement
décroît de 0.14 à 0.08 pour une masse volumique comprise de
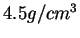 à
à 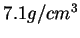 . Une telle évolution n'est pas sans
conséquence sur la capacité du matériau à s'écouler dans des
cavités de faibles épaisseurs et sur la prédiction des efforts.
Les distributions de densité en fin de remplissage (pièces Federal
Mogul) ou en fin de phase de transfert (pièce Dorst) sont très
probablement hétérogènes. Cette densité initiale est supposée
homogène dans l'ensemble de la cavité pour toutes les simulations.
Cette hypothèse ne tient pas compte de la faible amplitude
envisageable entre les valeurs extrêmes de la distribution de
densité au remplissage. Il est entendu que cette simplification
n'est pas sans conséquence sur le résultat numérique, son
influence est certainement peu importante dans le cas des pièces
Federal Mogul contrairement à la pièce Dorst.
Les déplacements mesurés, constitutifs de la base de données
d'entrée, sont également soumis à des imprécisions concernant la
détermination des hauteurs des pièces en fin de compression. Les
conséquences de ces imprécisions et la manière de traiter les
comparaisons sont commentées dans ce chapitre. Il ressort de
l'analyse proposée que les distributions de densité simulées et
surtout leurs gradients semblent bien reproduire les données
expérimentales pour les pièces mise en forme au sein de
l'entreprise Federal Mogul.
L'analyse des résultats permet, entre autres, la comparaison de deux
modèles de comportement de la poudre sur la base des répartitions
de densité après éjection et des efforts maximaux en fin de
compression. Il apparaît que le modèle de Drucker-Prager/Cap
modélise plus correctement le comportement des poudres de fer que
le modèle de CamClay, notamment pour l'aspect transfert de poudre
au cours de la compression. Il demeure que le modèle de
Drucker-Prager/Cap semble insuffisant pour décrire correctement
les gradients de densité développés au cours de la compression de
la pièce Dorst. Les valeurs des efforts simulés prédisent
correctement les efforts mesurés pour les pièces Federal Mogul et
la pièce Dorst dès lors que des écarts de 30% sont acceptés.
Moyennant les quelques corrections évoquées au cours de ce
chapitre (corrections de
. Une telle évolution n'est pas sans
conséquence sur la capacité du matériau à s'écouler dans des
cavités de faibles épaisseurs et sur la prédiction des efforts.
Les distributions de densité en fin de remplissage (pièces Federal
Mogul) ou en fin de phase de transfert (pièce Dorst) sont très
probablement hétérogènes. Cette densité initiale est supposée
homogène dans l'ensemble de la cavité pour toutes les simulations.
Cette hypothèse ne tient pas compte de la faible amplitude
envisageable entre les valeurs extrêmes de la distribution de
densité au remplissage. Il est entendu que cette simplification
n'est pas sans conséquence sur le résultat numérique, son
influence est certainement peu importante dans le cas des pièces
Federal Mogul contrairement à la pièce Dorst.
Les déplacements mesurés, constitutifs de la base de données
d'entrée, sont également soumis à des imprécisions concernant la
détermination des hauteurs des pièces en fin de compression. Les
conséquences de ces imprécisions et la manière de traiter les
comparaisons sont commentées dans ce chapitre. Il ressort de
l'analyse proposée que les distributions de densité simulées et
surtout leurs gradients semblent bien reproduire les données
expérimentales pour les pièces mise en forme au sein de
l'entreprise Federal Mogul.
L'analyse des résultats permet, entre autres, la comparaison de deux
modèles de comportement de la poudre sur la base des répartitions
de densité après éjection et des efforts maximaux en fin de
compression. Il apparaît que le modèle de Drucker-Prager/Cap
modélise plus correctement le comportement des poudres de fer que
le modèle de CamClay, notamment pour l'aspect transfert de poudre
au cours de la compression. Il demeure que le modèle de
Drucker-Prager/Cap semble insuffisant pour décrire correctement
les gradients de densité développés au cours de la compression de
la pièce Dorst. Les valeurs des efforts simulés prédisent
correctement les efforts mesurés pour les pièces Federal Mogul et
la pièce Dorst dès lors que des écarts de 30% sont acceptés.
Moyennant les quelques corrections évoquées au cours de ce
chapitre (corrections de  , des hauteurs en fin de
compression, introduction d'un coefficient de frottement évolutif
et d'une densité initiale hétérogène), il paraît possible de
conclure que les répartitions de densité et les efforts maximaux
en fin de compression pourraient être prédits avec une grande
précision pour les pièces Federal Mogul. Une simulation précise de
ces deux type de résultats pour la pièce Dorst semble conduire à
reconsidérer en plus la loi de comportement de la poudre.
La modélisation du comportement de la poudre constitue également
une approximation à la description du procédé. Cette approximation
a des conséquences plus fortes sur les résultats numériques au
travers du choix d'un des des modèles plutôt que par la mise en
, des hauteurs en fin de
compression, introduction d'un coefficient de frottement évolutif
et d'une densité initiale hétérogène), il paraît possible de
conclure que les répartitions de densité et les efforts maximaux
en fin de compression pourraient être prédits avec une grande
précision pour les pièces Federal Mogul. Une simulation précise de
ces deux type de résultats pour la pièce Dorst semble conduire à
reconsidérer en plus la loi de comportement de la poudre.
La modélisation du comportement de la poudre constitue également
une approximation à la description du procédé. Cette approximation
a des conséquences plus fortes sur les résultats numériques au
travers du choix d'un des des modèles plutôt que par la mise en
 uvre de données expérimentales différentes (trois chemins de
contrainte pour un essai de compression en matrice). Il s'avère
finalement que l'écoulement simulé est plus sensible au choix d'un
des deux modèles utilisés.
L'étude des effets des variations des données d'entrée n'est pas
menée de manière exhaustive au chapitre 6. En effet, ces
variations introduites aux modèles sont inhérentes aux résultats
des campagnes de mesure qui ont été spécifiquement menées pour
chaque type de pièce. La dernière remarque de cette conclusion en
rapport avec la sensibilité de l'écoulement n'est donc pas
réellement confirmée.
La poursuite de cette étude de sensibilité est exposée dans le
chapitre 7, elle porte sur les effets de variations imposées aux
paramètres du modèle de Drucker-Prager/Cap.
uvre de données expérimentales différentes (trois chemins de
contrainte pour un essai de compression en matrice). Il s'avère
finalement que l'écoulement simulé est plus sensible au choix d'un
des deux modèles utilisés.
L'étude des effets des variations des données d'entrée n'est pas
menée de manière exhaustive au chapitre 6. En effet, ces
variations introduites aux modèles sont inhérentes aux résultats
des campagnes de mesure qui ont été spécifiquement menées pour
chaque type de pièce. La dernière remarque de cette conclusion en
rapport avec la sensibilité de l'écoulement n'est donc pas
réellement confirmée.
La poursuite de cette étude de sensibilité est exposée dans le
chapitre 7, elle porte sur les effets de variations imposées aux
paramètres du modèle de Drucker-Prager/Cap.




suivant: Étude de sensibilité
monter: Pièces de validation
précédent: Résultats des simulations
Table des matières
FRACHON Arnaud
2002-11-12