| masse volumique |
zone 1 |
zone 2 |
zone 3 |
zone 4 |
zone 5 |
zone 6 |
zone 7 |
en 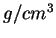 |
|
|
|
|
|
|
|
| mesures |
7.12 |
7.05 |
7.00 |
7.10 |
6.70 |
7.00 |
7.00 |
| 3S |
7.00 |
7.23 |
7.11 |
7.34 |
6.79 |
7.11 |
6.71 |
| Leicester |
7.01 |
7.21 |
7.12 |
7.38 |
6.78 |
7.13 |
6.76 |
| AEA |
7.01 |
7.18 |
7.16 |
7.35 |
6.75 |
7.13 |
6.87 |
| dispersion des |
0.12 |
0.18 |
0.16 |
0.25 |
0.09 |
0.13 |
0.29 |
| masses volumiques |
|
|
|
|
|
|
|
|
![\includegraphics[width=16.cm]{cartedorst.eps}](img841.png)
![\includegraphics[width=16.cm]{cartedorst.eps}](img841.png)
![\includegraphics[height=8cm]{resudorst.eps}](img843.png)
![\includegraphics[width=10cm]{compfordorst.eps}](img845.png)
![\includegraphics[height=9.cm]{dordensfor.eps}](img846.png)
![\includegraphics[width=16cm]{dorst2PQ.eps}](img847.png)
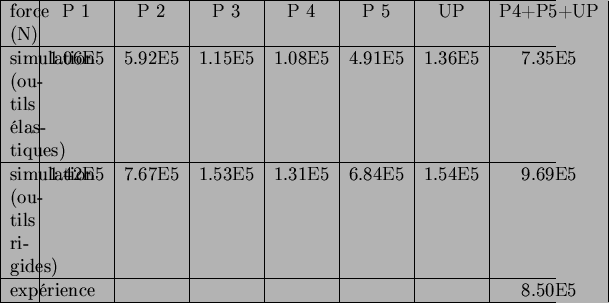
![\includegraphics[width=14.5cm]{dorelasvmt.eps}](img848.png)