



suivant: Les modules de l'ingénieur
monter: Élasticité linéaire isotrope
précédent: Élasticité linéaire isotrope
Table des matières
Pour cette partie, on se place dans le cas de l'élasticité
linéaire. Dans ces conditions, il existe une relation bi-univoque
entre la contrainte (de CAUCHY) et la déformation élastique
donnée par l'équation (3.3.1).
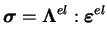 |
(3.19.1) |
On note que le tenseur
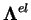 est d'ordre 4
et ne dépend ni de
est d'ordre 4
et ne dépend ni de
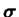 ni de
ni de
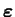 . Les composantes de ce tenseur
. Les composantes de ce tenseur
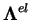 sont souvent exprimées en fonction de
sont souvent exprimées en fonction de 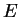 et
et 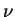 , appelés
les modules de l'ingénieur. L'élasticité isotrope correspond à une
même réponse du matériau considéré, quelque soit la direction de
sollicitation.La forme tensorielle est :
, appelés
les modules de l'ingénieur. L'élasticité isotrope correspond à une
même réponse du matériau considéré, quelque soit la direction de
sollicitation.La forme tensorielle est :
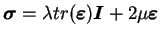 |
(3.19.2) |
Les relations entre les modules de l'ingénieur et les coefficients
de l'expression (3.3.2) sont les suivantes :
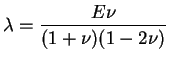 |
(3.19.3) |
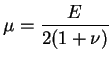 |
(3.19.4) |
L'avantage de cette écriture est de pouvoir déterminer le
potentiel par intégration de l'expression (3.3.2) dont le
résultat est :
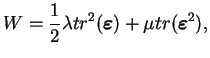 |
(3.19.5) |




suivant: Les modules de l'ingénieur
monter: Élasticité linéaire isotrope
précédent: Élasticité linéaire isotrope
Table des matières
FRACHON Arnaud
2002-11-12