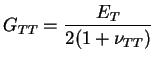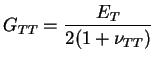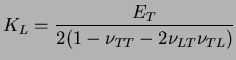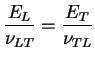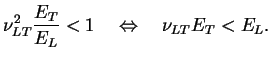suivant: Le potentiel
monter: Calage des paramètres
précédent: Cisaillement (directions 1-2)
Table des matières
Dans le plan d'isotropie du comportement orthotrope transverse, il
est possible de définir un module de cisaillement (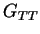 ) à
partir du module d'YOUNG (
) à
partir du module d'YOUNG (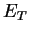 ) et du coefficient de POISSON
(
) et du coefficient de POISSON
(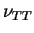 ) dans ce plan. Ce module de cisaillement est alors
donné par :
Il est également possible de définir un module de compression
latérale
) dans ce plan. Ce module de cisaillement est alors
donné par :
Il est également possible de définir un module de compression
latérale 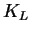 correspondant à un module volumique projeté dans le
plan d'isotropie.
Par ailleurs, il existe une relation entre les coefficients de
POISSON
correspondant à un module volumique projeté dans le
plan d'isotropie.
Par ailleurs, il existe une relation entre les coefficients de
POISSON 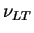 ,
,  et les modules d'YOUNG
et les modules d'YOUNG 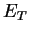 ,
, 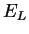 donnée par :
Cette relation indique le lien qu'il existe entre les directions
longitudinale et transversale au niveau des rapports de
déformations (les coefficients de POISSON).
Ces relations représentent un premier cadre pour la cohérence du
comportement vis a vis des principes physiques fondamentaux. Afin
de respecter ces principes, les domaines de valeurs des modules
sont restreintes. La première restriction considérée est d'ordre
logique ; les modules d'YOUNG les modules de cisaillement et le
module volumique doivent être positifs.
Cela signifie que la réponse du matériau à une sollicitation ne
lui est pas opposée. Par exemple, l'application d'une contrainte
de compression n'implique pas une augmentation de la dimension
dans la direction de sollicitation. Autre restriction qui découle de la première
est donnée par la relation suivante :
Cette relation indique notamment la direction longitudinale. Par
le jeu des relations entre les modules, il est également possible
de faire apparaître une restriction similaire sur le coefficient
donnée par :
Cette relation indique le lien qu'il existe entre les directions
longitudinale et transversale au niveau des rapports de
déformations (les coefficients de POISSON).
Ces relations représentent un premier cadre pour la cohérence du
comportement vis a vis des principes physiques fondamentaux. Afin
de respecter ces principes, les domaines de valeurs des modules
sont restreintes. La première restriction considérée est d'ordre
logique ; les modules d'YOUNG les modules de cisaillement et le
module volumique doivent être positifs.
Cela signifie que la réponse du matériau à une sollicitation ne
lui est pas opposée. Par exemple, l'application d'une contrainte
de compression n'implique pas une augmentation de la dimension
dans la direction de sollicitation. Autre restriction qui découle de la première
est donnée par la relation suivante :
Cette relation indique notamment la direction longitudinale. Par
le jeu des relations entre les modules, il est également possible
de faire apparaître une restriction similaire sur le coefficient
 . La dernière restriction concerne le plan d'isotropie,
classique pour le comportement élastique isotrope.
Ainsi, l'ensemble de ces relations et restrictions permettent notamment de
detecter les erreurs de détermination des coefficients.
. La dernière restriction concerne le plan d'isotropie,
classique pour le comportement élastique isotrope.
Ainsi, l'ensemble de ces relations et restrictions permettent notamment de
detecter les erreurs de détermination des coefficients.




suivant: Le potentiel
monter: Calage des paramètres
précédent: Cisaillement (directions 1-2)
Table des matières
FRACHON Arnaud
2002-11-12