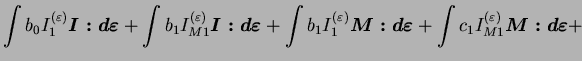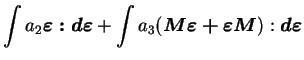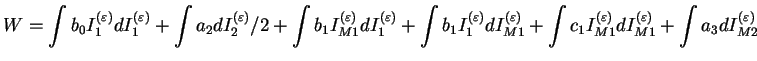suivant: Loi d'évolution des paramètres
monter: Élasticité non-linéraire orthotrope de
précédent: Relations et restrictions sur
Table des matières
Considérons l'élasticité orthotrope transverse exprimée par
l'équation (3.6.5).
On a vu que cette expression est intégrable du fait qu'elle dérive
d'un potentiel.
Soit,
ce qui donne en utilisant l'expression (3.6.5)
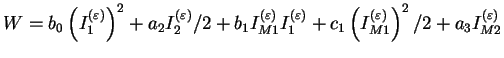 |
(3.22.9) |
Ce potentiel est représentatif d'un comportement élastique
orthotrope de révolution. Cette forme sera identifiable dans ce
qui suit et sera tenue pour responsable du comportement
anisotrope.
FRACHON Arnaud
2002-11-12
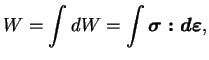
![$\displaystyle W = \int [(b_0 I_1^{(\varepsilon)} + b_1 I_{M1}^{(\varepsilon)})
...
...a_3 (\boldsymbol{M \varepsilon +
\varepsilon M})]: \boldsymbol{d\varepsilon}
$](img374.png)