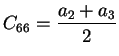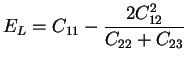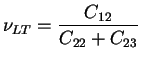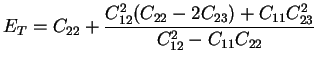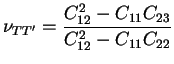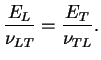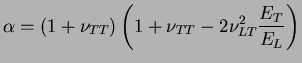suivant: Calage des paramètres
monter: Élasticité non-linéraire orthotrope de
précédent: Élasticité non-linéraire orthotrope de
Table des matières
Dans le cas de l'élasticité linéaire orthotrope de révolution,
Boehler [BOE97] a montré que la loi de comportement pouvait
s'écrire comme suit :
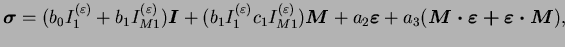 |
(3.22.5) |
avec
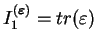 et
et
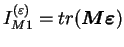 .
Or, la représentation classique fait état d'un tenseur d'ordre
quatre (3.6.6) plutôt qu'une combinaison de tenseurs
d'ordre deux (3.6.5).
.
Or, la représentation classique fait état d'un tenseur d'ordre
quatre (3.6.6) plutôt qu'une combinaison de tenseurs
d'ordre deux (3.6.5).
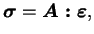 |
(3.22.6) |
avec
Or, il y a une correspondance entre les coefficients du tenseur
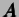 et les coefficients de l'équation (3.6.5).
Ce système d'équations peut être inversé afin d'exprimer les
coefficients du tenseur
et les coefficients de l'équation (3.6.5).
Ce système d'équations peut être inversé afin d'exprimer les
coefficients du tenseur  (matrice de rigidité) en fonction
des coefficients de l'équation (3.6.5) :
De plus, les coefficients de la matrice de rigidité peuvent
s'exprimer en fonction des modules de l'ingénieur de la façon
suivante :
Ainsi, on peut exprimer les modules de l'ingénieur en fonction des
coefficients de l'équation (3.6.5) :
(matrice de rigidité) en fonction
des coefficients de l'équation (3.6.5) :
De plus, les coefficients de la matrice de rigidité peuvent
s'exprimer en fonction des modules de l'ingénieur de la façon
suivante :
Ainsi, on peut exprimer les modules de l'ingénieur en fonction des
coefficients de l'équation (3.6.5) :
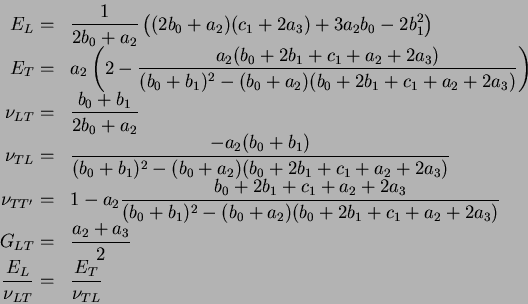 |
(3.22.7) |
De façon réciproque, il est possible d'exprimer les coefficients
de l'équation (3.6.5) en fonction des modules de
l'ingénieur.
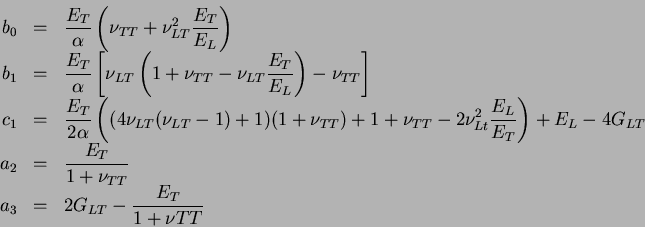 |
(3.22.8) |
avec
L'intérêt de cette écriture n'est pas immédiat, mais est très
utile dans la partie 3.7.2 page
![[*]](file:/usr/lib/latex2html/icons/crossref.png) qui suit.
qui suit.




suivant: Calage des paramètres
monter: Élasticité non-linéraire orthotrope de
précédent: Élasticité non-linéraire orthotrope de
Table des matières
FRACHON Arnaud
2002-11-12