



suivant: Cas linéaire
monter: Élasticité.
précédent: Élasticité linéaire orthotrope de
Table des matières
L'orthotropie de révolution implique que le comportement du
matériau possède une direction privilégiée, un axe de révolution
des symétries du comportement. Dans ce cas, la direction est
l'intersection des plans de symétries. Cette direction a été mise
en évidence dans les expériences présentées dans la section
2.7 page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Notons par
. Notons par 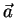 cette
direction privilégiée. Á partir de ce vecteur, il est possible
de construire un tenseur d'ordre deux associé à cette direction
dans l'espace des contraintes ou des déformations.
cette
direction privilégiée. Á partir de ce vecteur, il est possible
de construire un tenseur d'ordre deux associé à cette direction
dans l'espace des contraintes ou des déformations.
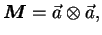 |
(3.22.1) |
où 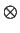 symbolise le produit tensoriel (
symbolise le produit tensoriel (
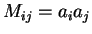 ).
Pour prendre en considération cette direction privilégiée dans la
loi de comportement, Boehler [BOE97] introduit dans
l'équation (3.4.29) le tenseur
).
Pour prendre en considération cette direction privilégiée dans la
loi de comportement, Boehler [BOE97] introduit dans
l'équation (3.4.29) le tenseur
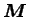 en
combinaison avec le tenseur des déformations ainsi que les
invariants qui en découlent. On obtient ainsi :
en
combinaison avec le tenseur des déformations ainsi que les
invariants qui en découlent. On obtient ainsi :
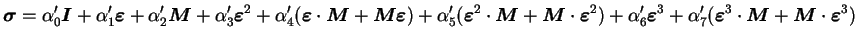 |
(3.22.2) |
En appliquant le théorème de Cayley-Hamilton 3.4, l'équation (3.6.2) devient :
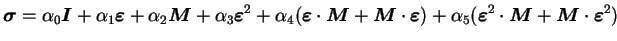 |
(3.22.3) |
où les coefficients 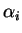 sont des combinaisons linéaires de
sont des combinaisons linéaires de
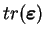 ,
,
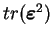 ,
,
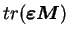 et
et
 .
En supposant que le solide soit hyperélastique, i.e. la
réponse mécanique
.
En supposant que le solide soit hyperélastique, i.e. la
réponse mécanique
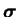 dérive de la fonction énergie de déformation W :
dérive de la fonction énergie de déformation W :
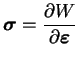 |
(3.22.4) |
avec
L'auteur en déduit une forme générale du comportement non-linéaire
orthotrope de révolution avec 13 constantes matériaux. Pour
pouvoir déterminer autant de paramètres, il faut beaucoup
d'expériences très précises.
Sous-sections




suivant: Cas linéaire
monter: Élasticité.
précédent: Élasticité linéaire orthotrope de
Table des matières
FRACHON Arnaud
2002-11-12