



suivant: Conclusion
monter: Expérience en laboratoire
précédent: Première synthèse sur les
Table des matières
Compression uniaxiale cyclique d'un comprimé
Afin de mettre en évidence les caractéristiques du comportement
élastique, des essais de compression simple sur des échantillons
cubiques ont été réalisés par Riera & al. [RPF$^+$00].
L'originalité de ces essais repose sur le caractère cyclique du
chargement au travers des nombreuses décharges-recharges de la
sollicitation imposée. Dans un premier temps, la poudre de fer
DISTALOY AE a été mise en forme par compression en matrice de
section carrée comme indiqué sur la figure 2.7.1. Un
repère est lié à l'échantillon de façon à mémoriser la direction
de compression. Des comprimés de différentes densités ont été
réalisés. Il est à noter que les échantillons ont été démoulés et
non pas éjectés de la matrice.
Figure 2.7.1:
Fabrication de l'échantillon dans une matrice de section
carrée
|
|
Le comportement de ces échantillons a ensuite été caractérisé
par un dispositif de compression uniaxiale. La contrainte
appliquée oscille entre zéro et un maximum croissant. La direction
de la sollicitation, par rapport au repère de mise en forme, est
l'une des variables de cet essai ainsi que le traduit la figure
2.7.2. Cette figure indique également l'ensemble de
mesures qui sont effectuées au cours des essais.
Figure 2.7.2:
Compression uniaxiale dans la direction de fabrication de
l'échantillon et dans la direction orthogonale
|
|
La figure 2.7.3 expose les mesures associées à un
essai complet représentatif de l'ensemble des résultats de la
campagne expérimentale. Les cycles de décharge-recharge en
contrainte présentent une ligne "enveloppe" (ligne pointillée).
Cette ligne enveloppe correspond à la réponse mécanique dans le
cas d'un chargement monotone jusqu'à la rupture. La réponse
expérimentale aux cycles de décharges-recharges montre clairement
par cette figure que les parties réversible et irréversible du
comportement ne peuvent être distinguées au travers d'un simple
chargement monotone. Cette première remarque constitue une des
conclusions majeures de cette campagne expérimentale.
Chacun des cycles de décharge-recharge permet d'isoler et
d'exhiber la partie réversible du comportement si elle existe
(courbe contraintes/déformations de décharge confondue avec celle
de la recharge). Ainsi l'identification est opérée au travers de
la décomposition de la déformation en une partie élastique et une
partie plastique. La déformation élastique étant nulle pour une
contrainte nulle, la déformation résiduelle pour cet état de
contraintes est donc plastique.
Figure 2.7.3:
Réponse dans un diagramme contrainte-déformation aux
sollicitations cycliques
|
|
Sur la figure 2.7.3, il apparaît de très légères
hystérésis sur les cycles. Ce phénomène, compte tenu de son
amplitude, ne sera pas pris en compte dans l'interprétation du
comportement du matériau. Il peut être dû en partie aux
imprécisions du dispositif de mesure. L'hypothèse proposée est
donc que les cycles correspondent à la partie élastique du
comportement du comprimé à vert.
La figure 2.7.4 illustre un faisceau de cycles
suite à l'élimination de la ligne associée au chargement monotone.
Figure 2.7.4:
Suppression de l'enveloppe élasto-plastique
|
|
La recherche d'un modèle élastique représentatif de ces cycles
réversibles conduit à relever deux points avant de conclure
l'analyse. L'une des propriétés du modèle recherché sera
d'associer à un état de déformations élastiques nul un état de
contraintes nul. Un autre point consiste à déterminer si au cours
d'un essai complet jusqu'à rupture (2.7.3) le
comportement réversible est identique. Ainsi pour chaque cycle, la
déformation permanente mesurée pour une contrainte nulle (fin de
la décharge) a été retirée. Cela revient à translater les cycles
représentés figure 2.7.4 à l'origine de l'axe de
déformation axiale. Ceci constitue l'origine des déformations
élastiques pour chaque cycle illustré par la figure
2.7.5.
Figure 2.7.5:
Diagramme déformation élastique-contrainte mettant en
évidence la superposition des cycles
|
|
Cette figure met également en évidence la superposition presque
parfaite des cycles. Cette remarque permet de conclure que le
comportement élastique n'est pas modifié par les déformations
plastiques croissantes enregistrées à chaque augmentation de la
contrainte axiale. Finalement cette figure représente dans notre
cadre idéalisé une seule courbe que l'on dénommera "réponse
élastique" par la suite.
Un autre point remarquable est que les comprimés ne présentent pas
de limite élastique en phase initiale de la compression. Ce
caractère spécifique est identifiable sur la figure
2.7.3 par la forme de la ligne enveloppe
pratiquement horizontale aux premiers stades de la compression
simple. Cette observation est systématique à l'ensemble des essais
menés. Les comprimés démoulés après densification en matrices se
déforment de manière permanente lorsqu'ils sont soumis à de très
faibles contraintes de compression simple : ceci suppose une
déformation des grains et plus probablement un réarrangement qui
modifie les contacts. Suite à une déformation plastique de l'ordre
de 1%, le comportement du comprimé correspond à une réponse du
type élasto-plastique écrouissable. Ceci met finalement en
évidence une grande sensibilité aux effets de trajet dans le
contexte où les modes de sollicitation changent brutalement.
Les essais de compression simple ont été pratiqués dans deux
directions comme indiqué sur la figure 2.7.2. Le
traitement des données exposé ci-dessus a été systématiquement
appliqué pour présenter les réponses élastiques. Les figures
2.7.6, 2.7.7 et 2.7.8 illustrent les réponses pour une
direction de contrainte parallèle et perpendiculaire à l'axe de
densification (fabrication du comprimé), ceci pour trois densités.
Figure 2.7.6:
Réponse axiale pour une densité de

|
|
Figure 2.7.7:
Réponse axiale pour une densité de
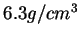
|
|
Figure 2.7.8:
Réponse axiale pour une densité de
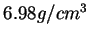
|
|
Cette série de résultats par compression simple de comprimés à vert
conduit à de nombreuses remarques. Il est à noter que ces réponses
en déformation-contrainte présentent une évolution avec la
densité. Le comportement élastique est non-linéaire et dépend de
l'orientation de la sollicitation par rapport au comprimé. La
non-linéarité du comportement élastique a déjà été observée par
Dawson & al. [DPB96], ce qui est illustré par la
figure 2.7.9. Cette figure met en lumière la
non-constance de la raideur non seulement pendant la compression
lorsque la masse volumique augmente, mais également à la décharge
des contraintes pour une densité approximativement constante.
Figure 2.7.9:
Évolution de la raideur (module d'Young) et de la masse
volumique en fonction de la pression appliquée lors d'une
compression dométrique par Dawson &
al.
|
|
Ainsi, la non-linéarité n'est pas le fait d'erreurs de mesures. En
outre, il ne faut pas oublier que le matériau étudié est un
assemblage de grains de poudre. Ce caractère non-linéaire de
l'élasticité a déjà été observé, non seulement pour les
assemblages de particules comme par exemple de l'argile (voir
CamClay exposé dans le chapitre 3), mais aussi pour
des assemblages de fibres de verre comme le montre Baudequin
& al. [BRR99]. Ces assemblages ont en commun la
non-cohésion entre les entités élémentaires qui les constituent et
une augmentation des surfaces de contact entre les entités lorsque
la contrainte de compression augmente.
Il est possible de comprendre ces phénomènes (non-linéarité et
dépendance de l'orientation) en considérant le problème de Hertz
[HER96]. Pour ce problème relatif à deux sphères en
contact, il apparaît que la raideur associée au rapprochement des
deux centres est fonction de la surface de contact entre les deux
sphères. En prolongeant ce raisonnement, il est possible de
déterminer l'origine de la dépendance de l'orientation. Pour cela,
le raisonnement s'appuie sur la figure 2.7.10 dont les
micrographies sont issues de [GER94].
Figure 2.7.10:
Évolution de la forme des grains au cours de la
compression en matrice. (A) au remplissage, (B) en cours de
compression, (C) densification complète
|
|
Les figures (A), (B) et (C) illustrent de manière simplifiée
l'évolution de la forme des grains au cours d'une compression en
matrices d'axe vertical. Ce schéma synoptique traite du stade
initial (A) suite au remplissage jusqu'au stade ultime (C) d'une
densité relative très élevée proche de 1. L'effet de l'orientation
de compression est pris en compte par l'évolution particulière des
surfaces de contact entre grains à la figure (B). Cette figure
signifie que dans la direction de compression la surface de
contact totale est plus importante pour un nombre de contacts
donné que dans la direction radiale qui lui est perpendiculaire.
Par extension à la solution du problème de Hertz, la raideur
suivant la direction de compression devrait être plus élevée que
la raideur suivant la direction perpendiculaire pour le cas (B).
Pour le schéma (C), la surface de contact entre grains est
similaire dans les deux directions, les raideurs devraient être
égales. Par ailleurs, cette illustration permet aussi de convenir
que la raideur devrait être une fonction croissante de la densité.
Si la compression simple uniaxiale permet une première
qualification des phénomènes élastiques propres aux comprimés à
vert, elle ne permet pas cependant de déterminer les valeurs
caractéristiques liées à ce phénomène pour des états de
confinement à contrainte élevée. En effet, la raideur mesurée,
portion rectiligne de la réponse à un cycle, est pour une densité
de  de 20 GPa alors que Dawson & al.
[DPB96] mesurent des raideurs de l'ordre de 200 GPa comme le
montre la figure 2.7.9. Par ailleurs, les mesures
réalisées par Pavier [PAV98] après confinement dans la
cellule triaxiale de révolution semblent confirmer les ordres de
grandeurs mesurés par Dawson. Il demeure parallèlement que les
mesures réalisées par Dawson et Pavier n'ont pas le degré de
précision pourtant nécessaire des essais menés par Riera. Ainsi,
la quantification de la non-linéarité et de l'anisotropie
élastique en fonction de la densité pour des états de confinement
à contrainte élevée devrait conduire à la conception de
dispositifs spéciaux et à la mise en place d'une campagne
expérimentale exhaustive.
Le niveau de précision requis pour la mesure de la réponse
élastique se justifie par l'allure des cycles. Ceux-ci sont
constitués d'une partie curviligne enregistrée aux faibles valeurs
de contraintes puis d'une portion rectiligne. Si la réponse d'un
cycle et une droite parallèle à la portion rectiligne
(comportement linéaire) sont reportés sur le même graphe, il est
aisé de comparer les écarts en déformation de ces deux types de
comportement pour une même contrainte. Cet écart est noté
(
de 20 GPa alors que Dawson & al.
[DPB96] mesurent des raideurs de l'ordre de 200 GPa comme le
montre la figure 2.7.9. Par ailleurs, les mesures
réalisées par Pavier [PAV98] après confinement dans la
cellule triaxiale de révolution semblent confirmer les ordres de
grandeurs mesurés par Dawson. Il demeure parallèlement que les
mesures réalisées par Dawson et Pavier n'ont pas le degré de
précision pourtant nécessaire des essais menés par Riera. Ainsi,
la quantification de la non-linéarité et de l'anisotropie
élastique en fonction de la densité pour des états de confinement
à contrainte élevée devrait conduire à la conception de
dispositifs spéciaux et à la mise en place d'une campagne
expérimentale exhaustive.
Le niveau de précision requis pour la mesure de la réponse
élastique se justifie par l'allure des cycles. Ceux-ci sont
constitués d'une partie curviligne enregistrée aux faibles valeurs
de contraintes puis d'une portion rectiligne. Si la réponse d'un
cycle et une droite parallèle à la portion rectiligne
(comportement linéaire) sont reportés sur le même graphe, il est
aisé de comparer les écarts en déformation de ces deux types de
comportement pour une même contrainte. Cet écart est noté
(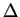 ) ainsi que l'illustre la figure 2.7.11.
) ainsi que l'illustre la figure 2.7.11.
Figure 2.7.11:
Erreur 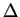 pour un même niveau de contrainte entre
un modèle élastique linéaire et non-linéaire
pour un même niveau de contrainte entre
un modèle élastique linéaire et non-linéaire
|
|
Cette figure met en évidence la différence en déformation si le
comportement élastique des comprimés à vert était supposé
linéaire, la raideur étant déterminée par la partie rectiligne de
la réponse mesurée. Or, dans le cadre d'une étude pour la
simulation d'un procédé de mise en forme "juste aux cotes", il est
nécessaire de prendre en compte la non-linéarité afin de ne pas
introduire une erreur d'amplitude (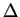 ) sur les retours
élastiques.
) sur les retours
élastiques.




suivant: Conclusion
monter: Expérience en laboratoire
précédent: Première synthèse sur les
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=6.5cm]{fabricare.eps}](img172.png)
![\includegraphics[width=6.5cm]{mesaniso.eps}](img173.png)
![\includegraphics[width=6.5cm]{purelas.eps}](img176.png)
![\includegraphics[height=8cm]{ultrason.eps}](img180.png)
![\includegraphics[height=9cm]{evolaniso.eps}](img181.png)
![\includegraphics[height=4cm]{nonlinear.eps}](img183.png)