Première synthèse sur les résultats d'essais

Les vitesses de déformations pratiquées en industrie sont comprises dans une gamme relativement réduite (de l'ordre de quelques cm/s à quelques dizaines de cm/s) (sauf applications particulières comme la compression dynamique). Pour cette gamme, les résultats expérimentaux n'ont pas mis en évidence de sensibilités notables du comportement à la compression. Ainsi, la vitesse de déformations ne constitue pas une variable influençant le comportement des poudres métalliques. Les relations qui relient les contraintes aux déformations seront supposées indépendantes du temps. Compte tenu de cette première remarque, les dispositifs préalablement décrits qui imposent des chargements quasi-statiques constituent des moyens de caractérisation fiables. Chacun d'entre eux permet de décrire des états de sollicitation distincts et des histoires de chargement spécifiques. Au cours de l'exposé concernant des résultats issus d'expériences en laboratoire, il semble apparaître que le nombre des variables pertinentes est, en première analyse, relativement restreint. Cette conclusion est valable dans le cadre de l'approche phénoménologique adoptée pour la simulation des phases de compression, de décharge et d'éjection. Ces variables sont la masse volumique, l'état de contraintes 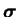$\boldsymbol{\sigma}$, l'état de déformation $\boldsymbol{\varepsilon}$ ainsi que l'ensemble des quantités issues de la représentation tensorielle, comme les invariants et les directions principales. Comme l'influence de la vitesse de déformations est maintenant exclue de notre analyse du comportement, les parties réversible et irréversible du comportement peuvent être respectivement qualifiées d'élastique et de plastique. La distinction entre l'élasticité et la plasticité est faite par la décomposition de l'état de déformations en une partie élastique et une partie plastique. Dans le cadre de la compression des poudres métalliques, les déformations plastiques sont très importantes (50% en volume pour les poudres de fer). Les déformations élastiques observées in situ sont très inférieures (<3% pour les poudres de fer). De telles considérations conduisent à considérer que les déformations élastiques observables sont négligeables par rapport aux déformations plastiques. La décomposition adoptée pour les déformations prend la forme de l'équation (2.6.1).

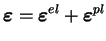$$\boldsymbol \varepsilon = \boldsymbol \varepsilon^{el} + \boldsymbol \varepsilon^{pl}$$ (2.14.1)

En première analyse, le phénomène élastique est supposé le premier à se manifester par application d'un chargement sur un comprimé à vert. La plasticité se manifeste ensuite si le chargement croit suffisamment. Cet hypothèse est dédiée au cycle de charge-décharge caractéristique du cycle de mise en forme (compression-éjection). Il convient de préciser en complément que le début de la compression est supposée s'opérer pour des caractéristiques élastiques très faibles, le début de la plastification intervenant pour des pressions de confinement de l'ordre de 1 MPa. Cette hypothèse sur l'ordre de manifestation de ces deux mécanismes conduit naturellement à adopter une modélisation très classique au comportement des matériaux. L'existence d'une "limite élastique" ou d'un "seuil plastique" est ainsi adoptée. Ceci conduira à définir des surfaces seuil fonction de l'état de contraintes. À l'exception du dispositif de compression triaxiale vraie^2.1 (et sauf cas très particulier), l'état de contraintes atteint et imposé par les essais de sollicitations homogènes peut être projeté dans un plan des contraintes P-Q. Cette représentation du comportement de la poudre peut être également adoptée dans le cadre des essais dits hétérogènes comme par exemple l'essai de densification par compression en matrices ou la compression diamétrale. Ainsi, pour l'ensemble des essais exploitables, la représentation des chemins de contraintes dans le plan P-Q est explicitée par les figures 2.6.1 et 2.6.2.

Figure 2.6.1: Représentation des chemins de contraintes pour la compression en matrice, la compression diamétrale, la compression uniaxiale et la traction uniaxiale dans un plan p-q

Figure 2.6.2: Représentation des chemins de contraintes possibles avec le dispositif de compression triaxiale de révolution dans un plan p-q

Les évolutions des états de contraintes sont directement déduites des chemins de contraintes subis par l'éprouvette. Dans l'espace de représentation des contraintes, ces chemins indiquent l'évolution des limites élastiques. La grande majorité des expériences décrites fournit des données quantitatives concernant le comportement plastique et la rupture en cours de chargement monotone. Cette absence presque systématique de la caractérisation précise de la contribution élastique est en partie due à de nombreuses difficultés (à caractère) technologiques. Il est possible de citer parmi celles-ci la faible amplitudes des déformations élastiques qui nécessite alors des dispositifs de mesures particulièrement précis. Concernant les expériences en rapport avec la densification, la contribution élastique est souvent négligée ce qui conduit à confondre les déformations totales aux déformations plastiques. Cette approximation sur les déformations semble validée par les amplitudes respectives des contributions élastique et plastique. La constitution d'une base de données fiable est dans son principe un point important pour la pratique de la simulation numérique. Dans cette optique, les données de trois centres de recherche ont été confrontées. Chacun d'entre eux a communiqué le résultat de ces mesures pour une compression en matrices. Ces informations concernent la caractérisation de la poudre de fer produite par la société Hägänas et identifiée sous l'appellation DISTALOY AE. Deux centres (AEA et 3S) ont réellement utilisé une matrice pour effectuer les mesures. Le troisième centre (Leicester) a réalisé un mode de chargement particulier en vue de reproduire, à l'aide d'un dispositif de compression triaxiale de révolution, les conditions d'un essai en matrices sans frottement. Les chemins de contraintes déduits des données issues de ces trois centres sont présentés sur la figure 2.6.3.

Figure 2.6.3: Résultats de la compression dométrique dans un plan p-q

Bien que ces trois centres étudient la même poudre avec un même type d'essai, la figure 2.6.3 présente des chemins de contraintes différents. Les données acquises au laboratoire 3S correspondent à un chemin de contraintes plus "déviatoire" que les deux autres centres. Par ailleurs, le chemin de contraintes déduit à partir des données du centre AEA tend vers un état de contraintes au caractère déviatoire décroissant en fin de compression. Avant de mener les essais, les trois centres ont utilisé la poudre sous une forme pulvérulente. Une variabilité de la densité de remplissage avant sollicitation est envisageable. Il demeure que la masse volumique initiale moyenne pour les trois centres devaient être de l'ordre de 3.1 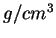$g/cm^3$. Au chemin de contraintes associé à l'application d'un chargement monotone croissant va correspondre une forte densification de la poudre de fer. Les différences déjà signalées s'expriment logiquement lorsque les trois points associés à une même masse volumique sont reportés dans le plan P-Q, ainsi que l'illustre la figure 2.6.4. La masse volumique représente indirectement une part de l'état de déformations.

Figure 2.6.4: Repérage d'une densité de comprimé pour une compression dométrique.

Pour une poudre et un type de chargement donnés, la relation entre les états de contraintes et de déformations doit être unique. Il est nécessaire de souligner que cela n'est pas réalisé ici, compte tenu de l'amplitude des écarts entre les trois courbes expérimentales. Cette disparité à propos de ces résultats relativement récents nécessite un travail d'analyse de la part des expérimentateurs pour comprendre de telles différences. Suite à la conclusion de ce débat, la définition d'un protocole standard pour l'obtention du chemin de contraintes lié à cet essai conduira à la constitution d'une base de données fiabilisée. En se référant à l'ensemble des dispositifs de densification, il est possible d'atteindre une même densité par divers chemins de contraintes comme cela est présenté par la figure 2.6.5.

Figure 2.6.5: Deux densités de comprimés de 6.5 et 7.1 pour un chemin dométrique et par des chemins triaxiaux de révolution

Cette figure met en évidence des états de contraintes différents pour une même densité au travers d'un nuage de points iso-densité. Ce nuage conduit à définir une surface fermée dans un espace de représentation des contraintes (par exemple l'espace des contraintes principales). Cette surface correspond à la surface de charge pour une densité fixée. L'essai triaxial de révolution est à cet égard à mettre en relief car il permet dans son principe d'explorer une partie significative du plan P-Q. Sur la figure 2.6.5, on note toutefois que les états de contraintes associés à la masse volumique 6.5 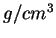$g/cm^3$, obtenus par compression en matrices et compression triaxiale de révolution respectivement, sont décalés. Ce décalage peut être attribué à la seule différence des dispositifs mis en uvre compte tenu des remarques déjà faites à propos de la comparaison des résultats en matrices issus des trois centres. Une première hypothèse concernant l'existence de difficultés pratiques pour obtenir une bonne reproductibilité du comportement entre essais peut donc être émise. Cependant, il demeure aussi que la figure 2.6.5 compare deux modes de sollicitations différents (essai triaxial de révolution et essai en matrices). Ainsi la différence enregistrée pourrait être aussi bien imputée à un effet de l'histoire de chargement. Ainsi, le décalage observé est imputable soit à une forte imprécision, soit à un comportement d'anisotropie fonction de l'histoire de chargement. Afin de pouvoir trancher, il serait intéressant de pouvoir pratiquer les essais suivants. L'influence éventuelle de différentes histoires de mises en forme a été analysée par Rottmann & al. [RCR01] par la fabrication de divers échantillons cylindriques. Nommons A, ceux obtenus par compression isotrope, et B ceux résultants d'une compression en matrices. Les comprimés à vert ainsi obtenus ont été ensuite placés au sein d'une cellule de compression triaxiale de révolution. Les sollicitations imposées par ce dispositif ont été suffisamment élevées pour augmenter les densités initiales des comprimés A et B. Les résultats de ces investigations sont présentés sous forme d'iso-densités par la figure 2.6.6 pour les spécimens A et par la figure 2.6.7 pour les échantillons B.

Figure 2.6.6: Évolution du seuil de plasticité par rapport à la densité relative pour un comprimé obtenu par compression isotrope (A) [RCR01]

Figure 2.6.7: Évolution de la limite élastique en fonction de la densité relative pour un échantillon mis en forme par compression en matrices (B) [RCR01]

Ces deux figures représentent des surfaces de charge en reliant par des courbes les points associés à une même densité. Ainsi ces courbes représentent, au sens de l'interprétation proposée, les seuils de limite d'élasticité pour chaque valeur de densité. Rappelons que ces courbes sont obtenues par combinaison d'une contrainte axiale et d'une contrainte radiale différentes, ce qui permet de parcourir le plan P-Q . Les points portés sur l'axe P correspondent au cas particulier du chargement isotrope, les contraintes radiale et axiale sont égales pour ce cas où seule la pression d'huile est imposée dans la cellule. Pour compléter la présentation d'une partie des résultats issus de l'article de Rottmann & al. [RCR01], une évolution du rapport entre les déformations radiale et axiale en fonction de la pression isotrope appliquée^2.2 est proposée sur la figure 2.6.8.

Figure 2.6.8: Évolution du rapport 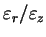$\varepsilon_r / \varepsilon_z$ au cours de la compression isotrope [RCR01]

Cette figure traite du cas particulier pour lequel les deux types de comprimés à vert ont été soumis à une pression isotrope au sein de la cellule (points de l'axe isotrope P) des figures 2.6.6 et 2.6.7. Afin d'identifier l'influence des histoires de mise en forme sur le comportement des comprimés à vert, les résultats des expérimentations doivent être analysés en vis-à-vis. Une remarque préliminaire et très générale au comportement des poudres est que les surfaces de charge sont en expansion dans le plan P-Q avec l'augmentation de la densité associée. Les figures 2.6.6 et 2.6.7 indiquent, par un pourcentage, la densité relative à la masse volumique du matériau dense. La comparaison de ces figures fait apparaître deux types de distinctions. La première concerne le niveau des contraintes requis pour atteindre une même densité. En effet, les échantillons A issus d'une pré-densification isotrope nécessitent des états de contraintes globalement inférieurs à ceux des échantillons B pour une même densité. La deuxième différence concerne la forme des courbes iso-densités à proximité de l'axe P des contraintes isotropes. Cette première comparaison met en lumière l'influence de l'histoire de la mise en forme sur la limite d'élasticité de la poudre. Ce protocole d'essais à chemin de densifications complexe nécessite quelques commentaires comparativement aux conditions industrielles de mise en forme. La séquence ordonnée des phases du procédé industriel sont la compression, la décharge puis l'éjection. L'ensemble des essais menés par Rottman conduit à une décharge complète des échantillons avant d'imposer un nouveau chemin de densifications. Ce protocole expérimental ne reproduit pas directement la séquence ordonnée des phases du procédé. La seconde remarque est que la variation de chemin imposée par les essais est discontinue si l'on considère le cas des comprimés pré-densifiés en matrice. Par ailleurs, la forme particulière des surfaces de charge à proximité de l'axe P s'estompe lorsque l'échantillon est faiblement re-densifié de 56 % à 58,8 %. La surface de charges évolue de sorte que l'axe P devienne une direction normale à cette surface pour une densité relative de 58,8 %. Ces essais confirment donc que le comportement plastique de massifs de poudres pré-densifiés est complexe. Ce fait expérimental est révélé par des chemins de chargement qui ne sont vraissemblablement pas proches des conditions de chargement industrielles. Les résultats illustrés par la figure 2.6.8 permettent de donner un autre éclairage de l'effet de l'histoire de déformation sur le comportement des comprimés sollicités de manière isotrope. Sur cette figure, le rapport des déformations axiale et radiale est de 1 pour les échantillons A. Ceci semble logique dans la mesure où les comprimés A ont été pré-densifiés par application d'une pression isotrope. Donc nulle direction particulière ne peut être identifiée. Ainsi, le comportement était et reste isotrope. Pour les échantillons B le rapport des déformations est par contre de l'ordre de 2. La direction axiale des échantillons B a une réponse en déformation différente de la direction radiale. La réponse et le comportement sous contrainte isotrope imposée n'est pas isotrope dans ce cas. Ceci indique que le comportement plastique est d'anisotropie induite par l'histoire de sollicitations. Cette dernière étant relatée au travers des déformations plastiques, il apparaît alors que l'anisotropie est corrélé aux déformations plastiques. L'influence de l'histoire du matériau sur son comportement apparaît également dans les travaux de Pavier [PAV98] pour des tests sur des échantillons normalement consolidés et sur-consolidés. Les résultats de ces deux types de chargement sont représentés et comparés sur la figure 2.6.9.

Figure 2.6.9: Limites élastiques pour des essais normalement consolidés et sur-consolidés

L'essai normalement consolidé consiste en une compression en deux temps dans un dispositif de compression triaxiale de révolution. Le premier temps consiste en une sollicitation isotrope en contrainte. Le deuxième temps superpose à cet état isotrope une contrainte uniaxiale. L'essai sur-consolidé se compose d'une étape de charge en sollicitation isotrope, suivi d'une décharge puis intervient finalement l'application d'une contrainte uniaxiale additionnelle. La figure 2.6.9 met nettement en évidence l'influence du chemin de contrainte sur la limite élastique. Ceci confirme les tendances des observations de Rottmann & al. [RCR01]. Mosbah [MOS95] a effectué la comparaison du comportement sur des échantillons pré-densifiés par compression en matrices et par compression isotrope. Les résultats de ces essais, ainsi que l'indique la figure 2.6.10, ont permis de mettre en évidence les différences de comportement. Les échantillons ont été sollicités par une compression simple monotone jusqu'à rupture. Ces tests ont été menés suivant deux directions relativement à l'orientation de l'échantillon.

Figure 2.6.10: Compression uniaxiale monotone sur des comprimés de mises en forme différente (en matrices et isotrope). Figure issue de la thèse de P. Mosbah

Cette figure confirme l'importance et l'effet de l'orientation du comprimé mis en forme par compression en matrices. Les mesures de Riera & al. [RPF$^+$00] sur les mêmes expériences indiquent les mêmes résultats ainsi que le montre la figure 2.6.11.

Figure 2.6.11: Compression uniaxiale monotone sur un comprimé mis en forme en matrice et testé suivant deux directions

Tant pour la figure 2.6.10 que pour la figure 2.6.11, le comportement du massif de poudre agglomérée est différent suivant l'orientation de la sollicitation par rapport à l'échantillon comprimé en matrice. Ces essais font apparaître les contraintes de rupture en compression uniaxiale pour chaque chargement monotone. Par ailleurs, des essais de rupture en traction ont été mis en uvre par Pavier [PAV98]. Il apparaît que la contrainte de rupture évolue avec la masse volumique comme l'illustre la figure 2.6.12.

Figure 2.6.12: Évolution de la contrainte de rupture en fonction de la masse volumique pour une poudre de fer

De plus, les niveaux de contraintes à la rupture sont particulièrement faibles par rapport aux niveaux atteints en compression uniaxiale ou encore en compression triaxiale de révolution. La faiblesse de ce niveau de contrainte peut être expliquée par les mécanismes qui engendrent la cohésion du massif de poudre après compression. D'un point de vue mécanique, les mécanismes principaux sont la cohésion entre grains en contact par adhérence et l'entrelacement des grains lorsque ceux-ci sont composés d'un matériau ductile. Ces mécanismes ne peuvent opposer qu'une faible résistance à la traction. Il est donc possible de voir apparaître des phénomènes singuliers propres aux poudres pré-densifiées, à savoir des déformations plastiques pour de faibles variations de contraintes pour un état de contraintes initial proche de zéro. Cela constitue un début d'explication au phénomène qui se produit pour les faibles contraintes en compression uniaxiale. Ces phénomènes sont propres aux comprimés à vert qui ne sont alors que des amas de grains faiblement cohésifs. Cette fragilité des liaisons inter-grains a été mise en relief par Riera & al. [RP01] par des traitements thermiques à différentes températures appliqués à des comprimés à vert. Ces températures sont comprises dans un intervalle de 250^&cir#circ;C à la température conseillée de frittage de 1100^&cir#circ;C. Suite à ces traitements thermiques, les échantillons sont soumis à une compression uniaxiale monotone. Il apparaît alors clairement que le comportement pour un état de contraintes faible tend progressivement vers celui du matériau dense tandis que la température de traitement augmente. L'échantillon qui a été fritté à la température de 1100^&cir#circ;C présente un comportement élasto-plastique classique des métaux denses. Les phénomènes présentés et les commentaires apportés à ce paragraphe sont en relation directe avec l'étude de nombreuses phases du procédé de compression à froid. Ils concernent essentiellement la phase de compression au travers des essais de densification de la poudre, la phase d'éjection au travers des essais de rupture. Ces essais ne sont pas, par leurs protocoles ou les phénomènes principaux mesurés, dédiés à l'analyse précise du rebond élastique de la pièce à vert en cours d'éjection. À l'occasion de cette thèse, une campagne expérimentale spécifique a été mise en uvre en collaboration avec l'université de Catalogne. L'objectif été de pouvoir enfin modéliser finement le comportement élastique lors des phases de décharge et d'éjection. La campagne expérimentale est exposée dans ce qui suit. La modélisation faisant l'objet du chapitre suivant.