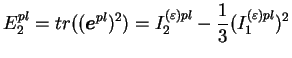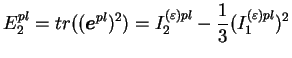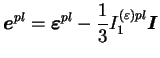suivant: Quantités équivalentes
monter: Élasticité non-linéraire orthotrope de
précédent: Le potentiel
Table des matières
Dans le cas qui nous préoccupe, l'anisotropie que l'on observe est
évolutive. En effet, lorsque l'on considère la poudre lâche, on
peut supposer sans trop d'erreur que le comportement est isotrope.
Donc, l'anisotropie apparaît avec la densification. Or, cette
densification du matériau est due aux phénomènes irréversibles. En
effet, si l'on suppose que la densification a pour source les
phénomènes réversibles et notamment l'élasticité, lorsque l'état
de contraintes est nul, la densification disparaîtrait. Donc,
seuls les phénomènes irréversibles et en particulier la plasticité
marque l'histoire du matériau.
Ainsi, il y a une évolution des paramètres de la loi élastique
fonction des phénomènes irréversibles. Parmi les paramètres de la
loi élastique, on distingue les paramètres qui forment
l'anisotropie et les autres qui sont liés à un comportement
isotrope. Les paramètres de l'anisotropie sont 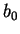 ,
, 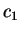 et
et
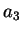 . Si la réponse plastique est isotrope, le comportement
élastique n'a pas de raison d'être anisotrope. On peut donc dire
que ces paramètres sont nuls, ce qui dégénère le modèle en une loi
isotrope. L'une des façons d'obtenir ce résultat est de faire
dépendre ces paramètres de la déformation déviatorique plastique
équivalente définit par :
On remarque que les paramètres
. Si la réponse plastique est isotrope, le comportement
élastique n'a pas de raison d'être anisotrope. On peut donc dire
que ces paramètres sont nuls, ce qui dégénère le modèle en une loi
isotrope. L'une des façons d'obtenir ce résultat est de faire
dépendre ces paramètres de la déformation déviatorique plastique
équivalente définit par :
On remarque que les paramètres 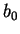 ,
, 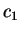 et
et 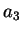 sont fonction
des premiers et second invariants des déformations plastiques.
En ce qui concerne les paramètres relatifs au comportement
sphérique (
sont fonction
des premiers et second invariants des déformations plastiques.
En ce qui concerne les paramètres relatifs au comportement
sphérique (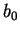 et
et 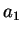 ), on peut supposer dans une première
approximation qu'ils dépendent du premier invariant des
déformations plastiques. Seules les données expérimentales peuvent
mettre en évidence cette dépendance.
Dans le cas d'une anisotropie plus générale, les paramètres
d'anisotropie peuvent dépendre de chacune des composantes du
tenseur des déformations plastiques.
L'ensemble de ces variations de l'anisotropie et de la
non-linéarité du comportement élastique peuvent être prises en
compte au travers de quantités qui permettent de simplifier les
relations. Ceci est l'objet de la section suivante qui introduit
la notion de quantités équivalentes et l'applique au cas de
l'élasticité non-linéaire orthotrope de révolution.
), on peut supposer dans une première
approximation qu'ils dépendent du premier invariant des
déformations plastiques. Seules les données expérimentales peuvent
mettre en évidence cette dépendance.
Dans le cas d'une anisotropie plus générale, les paramètres
d'anisotropie peuvent dépendre de chacune des composantes du
tenseur des déformations plastiques.
L'ensemble de ces variations de l'anisotropie et de la
non-linéarité du comportement élastique peuvent être prises en
compte au travers de quantités qui permettent de simplifier les
relations. Ceci est l'objet de la section suivante qui introduit
la notion de quantités équivalentes et l'applique au cas de
l'élasticité non-linéaire orthotrope de révolution.




suivant: Quantités équivalentes
monter: Élasticité non-linéraire orthotrope de
précédent: Le potentiel
Table des matières
FRACHON Arnaud
2002-11-12