next up previous contents
suivant: Cas général isotrope monter: Élasticité. précédent: Loi d'évolution des paramètres   Table des matières

Quantités équivalentes

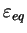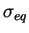Les quantités équivalentes sont définis comme étant duales dans le cadre de cette présentation. Dans le cadre de l'élasticité, ces quantités sont la déformation équivalente ( $ \varepsilon_{eq}$) et la contrainte équivalente ( $ \sigma_{eq}$) et sont liées par le travail élastique emmagasiné :

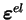$\displaystyle \textrm{travail emmagasiné} = \boldsymbol \sigma : \boldsymbol \varepsilon ^{el} = \sigma_{eq} \varepsilon_{eq}, $

où $ \boldsymbol \varepsilon ^{el}$ est la déformation élastique. En outre, il est supposé que la déformation dérive d'un potentiel et que la contrainte dérive du potentiel complémentaire. À partir de ces éléments, le cas isotrope est traité dans ce qui suit.
Sous-sections
FRACHON Arnaud 2002-11-12