



suivant: Conclusion
monter: Quantités équivalentes
précédent: Critiques des données expérimentales
Table des matières
Quel est l'intérêt de modéliser l'anisotropie puisque celle-ci
disparaît lorsque le matériau tend vers le matériau dense ? Pour
répondre à une telle question, il est nécessaire de bien situer le
contexte des expériences réalisées à cet effet. Les échantillons
qui ont été testés ne sont pas éjectés. Ainsi, les essais
représentent l'état du matériau au cours de la compression et non
après éjection. Cette différence semble importante, car pendant la
phase d'éjection, il est soupçonné que des phénomènes
irréversibles ont lieu. Donc, le modèle permet de prendre en
charge l'évolution de l'anisotropie au cours de la compression,
mais aussi après l'éjection. Cette capacité d'adaptation est
possible grâce à la flexibilité du modèle.
Ce modèle ne prend en compte que l'anisotropie orthotrope de
révolution. Cette symétrie est valable pour la compression d'un
cylindre avec un poinçon unique. Qu'en est-il pour les
compressions multi-poinçons ? Dans ce cas, l'anisotropie ne peut
a priori pas se résumer à une symétrie cylindrique.
Cependant, l'écriture du modèle peut être enrichie afin de tenir
compte de cette anisotropie plus compliquée. En effet, dans le cas
de l'orthotropie de révolution, la direction privilégiée est
repérée par un vecteur
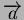 donne naissance au
tenseur
donne naissance au
tenseur
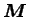 . Supposons dans un premier temps que le
comportement soit orthotrope. Il y a alors trois directions
privilégiées qui peuvent être repérées par trois vecteurs
. Supposons dans un premier temps que le
comportement soit orthotrope. Il y a alors trois directions
privilégiées qui peuvent être repérées par trois vecteurs
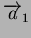 ,
,
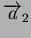 et
et
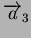 . Ces vecteurs donnent lieu aux trois
tenseurs
. Ces vecteurs donnent lieu aux trois
tenseurs
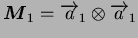 ,
,
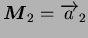
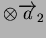 et
et
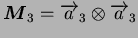 . Avec ces tenseurs et les invariants qui en découlent, il
est tout à fait concevable de construire un modèle orthotrope avec la même
méthodologie que celle ayant servi à construire le modèle
orthotrope de révolution. Il est ainsi possible d'obtenir une
anisotropie encore plus générale en gardant pour base les trois
vecteurs, mais en construisant des tenseurs combinant ces vecteurs
comme donnés par l'équation (3.7.14).
. Avec ces tenseurs et les invariants qui en découlent, il
est tout à fait concevable de construire un modèle orthotrope avec la même
méthodologie que celle ayant servi à construire le modèle
orthotrope de révolution. Il est ainsi possible d'obtenir une
anisotropie encore plus générale en gardant pour base les trois
vecteurs, mais en construisant des tenseurs combinant ces vecteurs
comme donnés par l'équation (3.7.14).
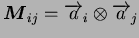 |
(3.23.14) |
La théorie peut ainsi être développée à l'anisotropie la plus générale
possible. Il reste que les investigations expérimentales seront
limitées du point de vue macroscopique, pour le calage des
coefficients d'un tel modèle de comportement dont le nombre
devient vite important. Il sera alors nécessaire
d'utiliser les approches micro-macromécaniques.
La véritable question est de savoir pourquoi l'anisotropie
élastique apparaît puis disparaît ? Pour répondre à cette
interrogation, il faut savoir ce qui donne naissance tant à
l'anisotropie qu'à la non-linéarité. Quelle est l'essence de ce
phénomène réversible ? La réversibilité du phénomène est due à
l'élasticité des grains. Quant à ce qui est des particularités de
non-linéarité et d'anisotropie, il faut chercher l'explication au
niveau des surfaces de contact inter-granulaires. D'une part, en
reprenant la théorie des contacts de Hertz, il est possible de
comprendre la non-linéarité. En effet, la surface de contact
augmentant, la raideur de l'ensemble augmente également. D'autre
part, si l'on considère la non-linéarité due à l'évolution de la
surface de contact entre grains, cela peut également expliquer
l'anisotropie. Pour cela, schématisons les grains de poudre par
des sphères. La figure 3.7.5 montre ces grains de
poudre à différents stades de la compression.
Figure 3.7.5:
Évolution de la forme des grains au cours de la
compression en matrice ainsi que de la surface de contact entre
grains. (A) au remplissage, (B) en cours de compression, (C)
densification complète
|
|
Le schéma indique une évolution différente des surfaces de
contacts selon la direction de déformation majeure et selon la
direction qui lui est perpendiculaire. Ce qu'il y a d'intéressant
dans cette schématisation, c'est qu'elle montre que
pour les densités relatives proches de 1, les grains sont aplatis,
mais les densités de surfaces de contact3.5 sont
identiques dans les deux directions.
Ainsi, afin de rendre compte de l'évolution de l'anisotropie au
travers des coefficients du modèle, ceux-ci doivent être fonction
des rapports de surfaces par rapport à chacune des trois
directions de l'espace.
Ces investigations sur l'anisotropie de l'élasticité constituent
un élément important dans la caractérisation du comportement des
poudres. Cette importance provient du lien entre l'anisotropie
élastique et l'anisotropie plastique évoquée par Böhlke
[BÖH01]. Il est alors possible de déterminer l'anisotropie
plastique au travers d'expériences mesurant l'anisotropie
élastique (ultrasons par exemple).




suivant: Conclusion
monter: Quantités équivalentes
précédent: Critiques des données expérimentales
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[height=9cm]{evolaniso.eps}](img181.png)