



suivant: Résultats du calage
monter: Application au cas de
précédent: Application au cas de
Table des matières
Dans le cas des poudres de fer, il apparaît, lors de la
compression uniaxiale, une non-linéarité pour les faibles états de
contraintes, puis une droite ainsi que l'illustre la figure
3.7.1.
Figure 3.7.1:
Pour les faibles niveaux de contraintes, il y a une
partie non-linéaire, puis une partie linéaire pour des contraintes
plus importantes
|
|
On suppose ainsi que le comportement élastique asymptotique est
linéaire. Cela signifit que la fonction de non-linéarité devant la
structure tensorielle tend vers 1 quand
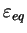 devient
grand. Ainsi, il ne reste plus que le comportement linéaire pour
lequel on peut déterminer les coefficients
devient
grand. Ainsi, il ne reste plus que le comportement linéaire pour
lequel on peut déterminer les coefficients 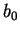 ,
, 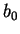 ,
, 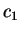 ,
,
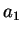 et
et 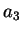 . Ces coefficients sont déterminés en utilisant les
modules de l'ingénieur rendus adimensionnels par division par
l'unité de contraintes. En effet, les coefficients
. Ces coefficients sont déterminés en utilisant les
modules de l'ingénieur rendus adimensionnels par division par
l'unité de contraintes. En effet, les coefficients 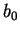 ,
, 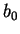 ,
,
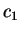 ,
, 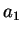 et
et 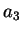 sont adimensionnels de façon à ce que la
déformation équivalente ait la dimension d'une déformation. Une
fois en possession de ces coefficients, il est alors possible de
déterminer la fonction de non-linéarité.
Afin de déterminer les valeurs des coefficients
sont adimensionnels de façon à ce que la
déformation équivalente ait la dimension d'une déformation. Une
fois en possession de ces coefficients, il est alors possible de
déterminer la fonction de non-linéarité.
Afin de déterminer les valeurs des coefficients 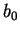 ,
, 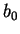 ,
,
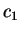 ,
, 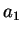 et
et 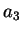 , on utilise l'équation 3.6.8. Les
modules de l'ingénieur que l'on va considérer seront rendus
adimensionnels par l'unité de contraintes afin d'obtenir des
coefficients pour la déformation équivalente homogène à une
déformation. Ainsi, les modules d'Young adimensionnels sont notés
, on utilise l'équation 3.6.8. Les
modules de l'ingénieur que l'on va considérer seront rendus
adimensionnels par l'unité de contraintes afin d'obtenir des
coefficients pour la déformation équivalente homogène à une
déformation. Ainsi, les modules d'Young adimensionnels sont notés
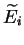 pour ne pas les confondre avec les modules
d'élasticité dont la dimension est homogène à une contrainte.
Cependant, les lettres utilisées coïncident car la signification
des quantités est semblable. En l'occurrence, ces modules
adimensionnels indiquent d'une part le rapport d'anisotropie, et
d'autre part le module asymptotique.
pour ne pas les confondre avec les modules
d'élasticité dont la dimension est homogène à une contrainte.
Cependant, les lettres utilisées coïncident car la signification
des quantités est semblable. En l'occurrence, ces modules
adimensionnels indiquent d'une part le rapport d'anisotropie, et
d'autre part le module asymptotique.




suivant: Résultats du calage
monter: Application au cas de
précédent: Application au cas de
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[height=4cm]{nonlinear.eps}](img183.png)
![\includegraphics[height=4cm]{nonlinear.eps}](img183.png)