



suivant: Calage des paramètres
monter: Quantités équivalentes
précédent: Cas général isotrope
Table des matières
Application au cas de l'élasticité orthotrope de révolution
non-linéaire
Pour cette application, le tenseur Z sera le tenseur des
déformations et le tenseur dual sera le tenseur des contraintes.
Pour ce cas, le potentiel sera noté W. On définit la déformation
équivalente comme suit :
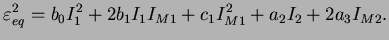 |
(3.23.10) |
De façon similaire à l'équation (3.7.2), on a :
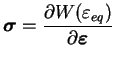 |
(3.23.11) |
En utilisant la déformation équivalente (3.7.10) dans
l'équation (3.7.11), on obtient :
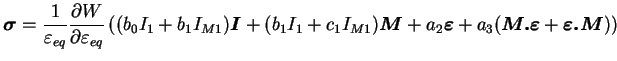 |
(3.23.12) |
Cette équation (3.7.12) montre une multiplication entre une
fonction scalaire et une structure tensorielle. La structure
tensorielle n'est autre que la loi de comportement élastique
orthotrope de révolution linéaire. Ainsi, la fonction scalaire
peut permettre de rendre non-linéaire la loi de comportement
élastique. Dans le cas où l'expression du potentiel est
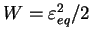 , le modèle ainsi obtenu n'est autre que
celui de l'élasticité linéaire orthotrope de révolution. Étant
donné que le comportement asymptotique est linéaire (tend à être
linéaire lorsque
, le modèle ainsi obtenu n'est autre que
celui de l'élasticité linéaire orthotrope de révolution. Étant
donné que le comportement asymptotique est linéaire (tend à être
linéaire lorsque
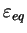 devient grand), le potentiel
doit faire intervenir le terme
devient grand), le potentiel
doit faire intervenir le terme
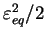 . Les
résultats d'expériences dégagent la forme donnée par l'équation
3.7.13 pour le potentiel proposé par Frachon &
al. [FID$^+$01].
. Les
résultats d'expériences dégagent la forme donnée par l'équation
3.7.13 pour le potentiel proposé par Frachon &
al. [FID$^+$01].
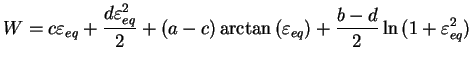 |
(3.23.13) |
Ce modèle ainsi exprimé, généralise le comportement élastique dans
la limite de l'orthotropie de révolution. Cette généralité englobe
l'élasticité linéaire isotrope, non-linéaire isotrope et linéaire
orthotrope de révolution ainsi que le montre le tableau
3.7.1.
Tableau 3.7.1:
flexibilité du modèle non-linéaire orthotrope de
révolution
 |
Sous-sections




suivant: Calage des paramètres
monter: Quantités équivalentes
précédent: Cas général isotrope
Table des matières
FRACHON Arnaud
2002-11-12