suivant: Application au cas de
monter: Quantités équivalentes
précédent: Quantités équivalentes
Table des matières
Pour l'explication de cette technique des quantités équivalentes,
on considère le tenseur
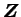 et son dual, le tenseur
et son dual, le tenseur
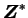 . On commence par définir une quantité
équivalente
. On commence par définir une quantité
équivalente 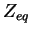 par :
par :
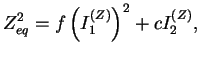 |
(3.23.1) |
où
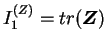 et
et
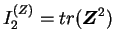 .
On suppose que le tenseur dual dérive d'un potentiel
.
On suppose que le tenseur dual dérive d'un potentiel 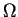 fonction de
fonction de 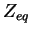 .
.
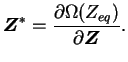 |
(3.23.2) |
Ce qui donne en d'autres termes :
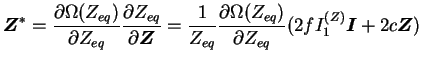 |
(3.23.3) |
Ainsi, il est possible de déterminer la quantité équivalente duale
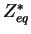 . Pour cela, il faut dans un premier temps, définir les
invariants du tenseur dual. Soit
. Pour cela, il faut dans un premier temps, définir les
invariants du tenseur dual. Soit
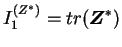 et
et
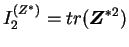 ces invariants.
ces invariants.
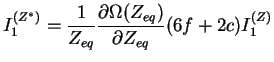 |
(3.23.4) |
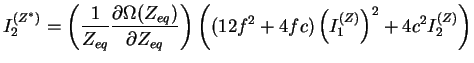 |
(3.23.5) |
En prenant le carré de l'équation (3.7.4), on arrive à :
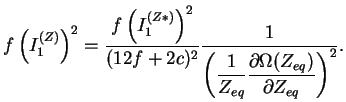 |
(3.23.6) |
Et l'équation (3.7.5) nous conduit à :
 |
(3.23.7) |
En utilisant les équations (3.7.6) et (3.7.7) dans
l'expression (3.7.1), on a :
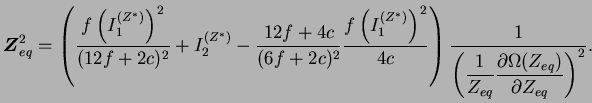 |
(3.23.8) |
En plaçant l'équation (3.7.8) dans la définition
(3.7.2), on a finalement :
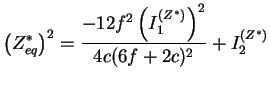 |
(3.23.9) |
Il est ainsi établi la quantité équivalente complémentaire en
fonction des invariants du tenseur dual. Ceci met en lumière la
capacité d'inversion de ces relations. Ainsi, le potentiel à la
possibilité d'être exprimé en fonction de l'une ou de l'autre des
quantités équivalentes.
Cette technique est élargie à l'orthotropie de révolution
non-linéaire dans le cas d'un modèle élastique ainsi qu'il est
exposé par la suite.




suivant: Application au cas de
monter: Quantités équivalentes
précédent: Quantités équivalentes
Table des matières
FRACHON Arnaud
2002-11-12