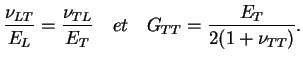suivant: Élasticité non-linéraire orthotrope de
monter: Élasticité.
précédent: Hyperélasticité non-linéaire isotrope
Table des matières
L'une des caractéristiques qui a été observée dans la section
2.7 page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) est l'anisotropie. La forme
de l'échantillon testé n'autorisait que l'appliquation de
sollicitations axisymétriques. Le type même de sollicitations à
conduit à supposer que le comportement est orthotrope de
révolution. Afin de prendre en compte la particularité de ce
comportement, il est dans un premier temps exposé un modèle
d'élasticité linéaire orthotrope de révolution. L'objectif de la
présentation de ce modèle est de pouvoir observer les différences
avec un modèle linéaire isotrope ainsi que la prise en compte de
la direction privilégiée.
Il est entendu que ce modèle n'est pas en mesure de modéliser le
comportement élastique des poudres de fer mises en forme par
compression en matrices.
L'orthotropie de révolution est une sous-classe d'orthotropie qui
se caractérise par un plan d'isotropie en chaque point du
matériau. La normale à ce plan correspond à l'axe de révolution
des symétries du groupe
est l'anisotropie. La forme
de l'échantillon testé n'autorisait que l'appliquation de
sollicitations axisymétriques. Le type même de sollicitations à
conduit à supposer que le comportement est orthotrope de
révolution. Afin de prendre en compte la particularité de ce
comportement, il est dans un premier temps exposé un modèle
d'élasticité linéaire orthotrope de révolution. L'objectif de la
présentation de ce modèle est de pouvoir observer les différences
avec un modèle linéaire isotrope ainsi que la prise en compte de
la direction privilégiée.
Il est entendu que ce modèle n'est pas en mesure de modéliser le
comportement élastique des poudres de fer mises en forme par
compression en matrices.
L'orthotropie de révolution est une sous-classe d'orthotropie qui
se caractérise par un plan d'isotropie en chaque point du
matériau. La normale à ce plan correspond à l'axe de révolution
des symétries du groupe
 évoqué dans la section
3.2.3 en page
évoqué dans la section
3.2.3 en page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Si on prend dans un
repère rectangulaire le plan défini par les directions 1 et 2
comme plan d'isotropie alors, il y a cinq modules de l'ingénieur
pour décrire ce modèle :
où l'indice T signifie "Transverse à l'axe de révolution" et L
signifie "Longitudinal à cet axe". Une expression de la relation
entre déformation et contrainte est donnée par l'équation
(3.5.1) :
. Si on prend dans un
repère rectangulaire le plan défini par les directions 1 et 2
comme plan d'isotropie alors, il y a cinq modules de l'ingénieur
pour décrire ce modèle :
où l'indice T signifie "Transverse à l'axe de révolution" et L
signifie "Longitudinal à cet axe". Une expression de la relation
entre déformation et contrainte est donnée par l'équation
(3.5.1) :
 |
(3.21.1) |
Avec :
En considérant les composantes correspondant aux diagonales des
tenseurs de déformations et de contraintes, il est possible de
remarquer l'emprunte de l'axe de révolution (direction de
compression 33) et le plan d'isotropie (plan de cisaillement 12).
Ce type de définition semble plus approprié à notre problème,
notamment pour les pièces axi-compressées, la direction
longitudinale correspondant à l'axe de compression. Cependant, ce
type de modèle ne permet pas de prendre en compte le caractère
non-linéaire. Ceci fait l'objet de la section suivante.




suivant: Élasticité non-linéraire orthotrope de
monter: Élasticité.
précédent: Hyperélasticité non-linéaire isotrope
Table des matières
FRACHON Arnaud
2002-11-12