Matériaux anisotropes

suivant: Élasticité linéaire isotrope monter: Isotropie-Anisotropie précédent: Matériaux isotropes Table des matières

Matériaux anisotropes

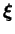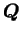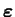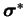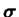Un matériau est dit anisotrope si lorsque l'on transforme le tenseur de structure $\boldsymbol \xi$ par une transformation orthogonale $\boldsymbol Q$ et gardant le même tenseur $\boldsymbol \varepsilon$ , alors, en général, la réponse ainsi transformée $\boldsymbol \sigma ^*$ est différente de la réponse avant transformation $\boldsymbol \sigma$ :

$\displaystyle \boldsymbol \sigma ^* = \boldsymbol \Psi ( \boldsymbol \varepsil... ...ol Q \cdot \boldsymbol \xi \cdot \boldsymbol Q ^T ) \neq \boldsymbol \sigma.$

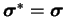Il faut alors chercher un ensemble de transformations pour lesquelles on a $\boldsymbol \sigma^* = \boldsymbol \sigma$ .

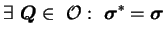$\displaystyle \exists \boldsymbol Q \in \mathcal O : \boldsymbol \sigma ^* = \boldsymbol \sigma$

(3.18.5)

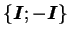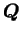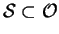Si les seules transformations qui vérifient l'équation (3.2.5) sont $\{\boldsymbol I ; -\boldsymbol I \}$ , alors le matériau est dit d'anisotropie générale. Par contre, s'il existe d'autres transformations $\boldsymbol Q$ qui vérifient (3.2.5), ces transformations constituent un sous-groupe $\mathcal S \subset \mathcal O$ . 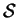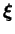Ce sous-groupe $\mathcal S$ est appelé groupe des symétries du matériau et est un groupe d'invariances du tenseur de structure $\boldsymbol \xi$ qui s'exprime par l'équation (3.2.6).

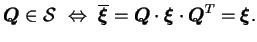$\displaystyle \boldsymbol Q \in \mathcal S \Leftrightarrow \ \overline{\bold... ...\boldsymbol Q \cdot \boldsymbol \xi \cdot \boldsymbol Q ^T = \boldsymbol \xi .$

(3.18.6)

En considérant l'équation (3.2.6) et le principe d'isotropie de l'espace, on est conduit à l'équation (3.2.7).

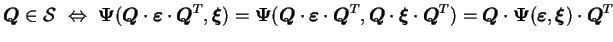$\displaystyle \boldsymbol Q \in \mathcal S \Leftrightarrow \boldsymbol \Psi... ...symbol \Psi ( \boldsymbol \varepsilon , \boldsymbol\xi) \cdot \boldsymbol Q ^T$

(3.18.7)

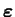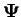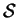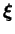L'équation (3.2.7) signifie que, par rapport à $\boldsymbol \varepsilon$ , la fonction $\boldsymbol \Psi$ est invariante dans le sous-groupe $\mathcal S$ et seulement dans ce groupe. Finalement, pour un matériau anisotrope, le groupe d'invariance du tenseur de structure $\boldsymbol \xi$ est identique au groupe de transformations qui caractérise les symétries du corps. En conséquence, pour l'écriture des lois de comportement anisotropes, le tenseur de structure apparaît explicitement dans la formulation tensorielle du modèle de comportement.

suivant: Élasticité linéaire isotrope monter: Isotropie-Anisotropie précédent: Matériaux isotropes Table des matières

FRACHON Arnaud 2002-11-12