



suivant: Matériaux anisotropes
monter: Isotropie-Anisotropie
précédent: Principe d'isotropie de l'espace
Table des matières
Un matériau est dit isotrope si en appliquant une quelconque
transformation
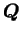 d'un groupe orthogonal
d'un groupe orthogonal
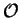 au matériau mais pas au tenseur
au matériau mais pas au tenseur
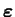 , la
réponse
, la
réponse
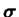 est la même. Ceci est exprimé par
l'équation (3.2.3).
est la même. Ceci est exprimé par
l'équation (3.2.3).
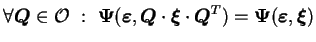 |
(3.18.3) |
Cette équation indique que le tenseur de structure est un tenseur
isotrope :
Ainsi, pour un matériau isotrope, l'équation constitutive
(3.2.1) est réduite à :
Une conséquence directe de cette définition est que les directions
principales du tenseur
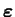 sont les mêmes
que celles du tenseur
sont les mêmes
que celles du tenseur
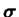 . Afin de mettre en
évidence cette coïncidence des directions principales, considérons
une réflexion
. Afin de mettre en
évidence cette coïncidence des directions principales, considérons
une réflexion
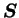 (cas particulier de
(cas particulier de
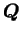 )
par rapport à l'une des directions principales de
)
par rapport à l'une des directions principales de
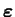 que l'on notera
que l'on notera 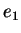 . Cette transformation est
appliquée à la fois au tenseur
. Cette transformation est
appliquée à la fois au tenseur
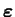 et au
tenseur de structure
et au
tenseur de structure
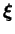 . La réponse d'une telle
transformation reste inchangée puisque le matériau est isotrope.
De plus, en appliquant le principe d'isotropie de l'espace, il
vient :
. La réponse d'une telle
transformation reste inchangée puisque le matériau est isotrope.
De plus, en appliquant le principe d'isotropie de l'espace, il
vient :
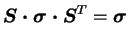 |
(3.18.4) |
L'équation (3.2.4) implique que la direction 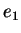 est
principale pour le tenseur
est
principale pour le tenseur
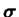 . Donc, finalement,
les directions principales de
. Donc, finalement,
les directions principales de
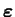 et de
et de
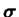 sont les mêmes.
La conséquence pour l'expression des lois de comportement est
l'absence de tenseur de structure.
sont les mêmes.
La conséquence pour l'expression des lois de comportement est
l'absence de tenseur de structure.




suivant: Matériaux anisotropes
monter: Isotropie-Anisotropie
précédent: Principe d'isotropie de l'espace
Table des matières
FRACHON Arnaud
2002-11-12