



suivant: Principe d'isotropie de l'espace
monter: Élasticité.
précédent: Introduction
Table des matières
Considérons la relation
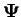 entre tenseurs du
second ordre donnée par l'équation (3.2.1), où
entre tenseurs du
second ordre donnée par l'équation (3.2.1), où
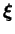 est un tenseur de structure caractéristique au
matériau,
est un tenseur de structure caractéristique au
matériau,
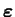 est le tenseur des
déformations élastiques et
est le tenseur des
déformations élastiques et
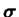 est le tenseur des contraintes.
est le tenseur des contraintes.
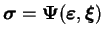 |
(3.18.1) |
Dans le cas le plus général, les directions propres de
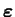 et celles de
et celles de
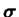 sont
différentes.
sont
différentes.
Sous-sections
FRACHON Arnaud
2002-11-12