



suivant: Matériaux isotropes
monter: Isotropie-Anisotropie
précédent: Isotropie-Anisotropie
Table des matières
Les équations constitutives sont soumises à l'invariance que
requiert le Principe d'Isotropie de l'Espace (ou Principe
d'Indifférence Matériel). En d'autres termes, le choix d'un repère
dans l'espace n'a pas d'influence sur les équations constitutives.
Une conséquence de ce principe est qu'une transformation
quelconque
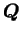 d'un groupe orthogonal
d'un groupe orthogonal
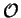 appliquée à la fois au repère et au tenseur
appliquée à la fois au repère et au tenseur
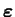 implique une réponse identiquement transformée du
tenseur
implique une réponse identiquement transformée du
tenseur
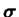 . Une telle transformation est
exprimée sur l'équation (3.2.1). La transformation
de cette équation (3.2.1) est donnée par l'équation
(3.2.2).
. Une telle transformation est
exprimée sur l'équation (3.2.1). La transformation
de cette équation (3.2.1) est donnée par l'équation
(3.2.2).
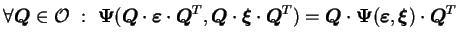 |
(3.18.2) |
Cette équation (3.2.2) montre l'invariance de la fonction
tensorielle
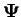 par rapport à ces deux arguments.
Ainsi, le choix du repère n'a pas d'incidence sur l'écriture du
modèle de comportement.
par rapport à ces deux arguments.
Ainsi, le choix du repère n'a pas d'incidence sur l'écriture du
modèle de comportement.
FRACHON Arnaud
2002-11-12