



suivant: Élasticité linéaire orthotrope de
monter: Élasticité non-linéaire isotrope
précédent: G est constant
Table des matières
Il est possible de représenter le tenseur des contraintes comme
étant une fonction du tenseur des déformations, dans le cas où
l'on ne considère pas l'anisotropie du matériau. Cette fonction du
tenseur des déformations a la possibilité d'être exprimée sous
forme d'une suite pôlynomiale :
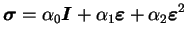 |
(3.20.29) |
Les coefficients 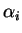 sont fonctions des invariants du
tenseur des deformations (
sont fonctions des invariants du
tenseur des deformations (
 et
et
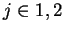 ).
On suppose que le comportement est hyperélastique. Donc, le
tenseur des contraintes dérive d'un potentiel W de la façon
suivante :
).
On suppose que le comportement est hyperélastique. Donc, le
tenseur des contraintes dérive d'un potentiel W de la façon
suivante :
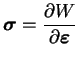 |
(3.20.30) |
Ce potentiel W dépend des invariants du tenseur des déformations.
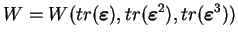 |
(3.20.31) |
En tenant compte de l'équation (3.4.31) dans l'équation
(3.4.30), on obtient pour le tenseur des contraintes :
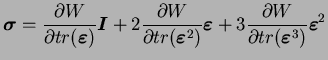 |
(3.20.32) |
Dans un état de référence non distordu (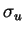 correspondant à
la non sollicitation), on a :
Si de plus, cet état de référence est l'état naturel, alors :
correspondant à
la non sollicitation), on a :
Si de plus, cet état de référence est l'état naturel, alors : 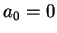 .
La condition d'intégrabilité ou théorème de Shwartz donne les
relations
suivantes :
.
La condition d'intégrabilité ou théorème de Shwartz donne les
relations
suivantes :
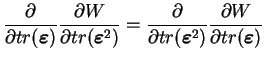 |
(3.20.33) |
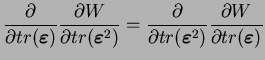 |
(3.20.34) |
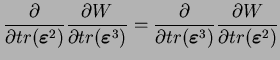 |
(3.20.35) |
L'équation (3.4.33) donne
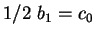 , l'équation
(3.4.34) donne
, l'équation
(3.4.34) donne 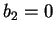 , et l'équation (3.4.35) donne
, et l'équation (3.4.35) donne
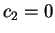 .
Ainsi, dans le cas de l'hyperélasticité non-linéraire isotrope, le
tenseur des contraintes a pour expression en fonction du tenseur
des déformations :
.
Ainsi, dans le cas de l'hyperélasticité non-linéraire isotrope, le
tenseur des contraintes a pour expression en fonction du tenseur
des déformations :
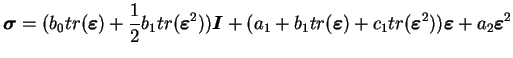 |
(3.20.36) |
Les constantes 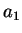 ,
, 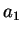 ,
, 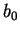 ,
, 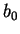 ,
, 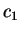 et
et 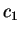 seront déterminées à
partir des résultats expérimentaux (compression simple,
compression triaxiale).
Ces constantes n'en restent pas moins des fonctions d'une variable interne qui
peut être par exemple la densité3.2 ou la déformation volumique plastique3.3.
Dans cette modélisation, il y a 6 constantes à déterminer pour
pouvoir décrire le caractère non-linéaire. Ce nombre important de
constantes implique des difficultés à les caler. L'ensemble de ces constantes
étant toutes homogènes à une contrainte. De plus, les coefficients sont
difficiles à interpréter.
Cependant, cette proposition de modèle présente l'avantage de
dériver d'un potentiel, prenant en compte la conservation de
l'énergie. C'est donc cette procédure qui sera retenue pour établir
le modèle élastique non-linéaire anisotrope.
seront déterminées à
partir des résultats expérimentaux (compression simple,
compression triaxiale).
Ces constantes n'en restent pas moins des fonctions d'une variable interne qui
peut être par exemple la densité3.2 ou la déformation volumique plastique3.3.
Dans cette modélisation, il y a 6 constantes à déterminer pour
pouvoir décrire le caractère non-linéaire. Ce nombre important de
constantes implique des difficultés à les caler. L'ensemble de ces constantes
étant toutes homogènes à une contrainte. De plus, les coefficients sont
difficiles à interpréter.
Cependant, cette proposition de modèle présente l'avantage de
dériver d'un potentiel, prenant en compte la conservation de
l'énergie. C'est donc cette procédure qui sera retenue pour établir
le modèle élastique non-linéaire anisotrope.




suivant: Élasticité linéaire orthotrope de
monter: Élasticité non-linéaire isotrope
précédent: G est constant
Table des matières
FRACHON Arnaud
2002-11-12