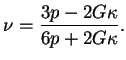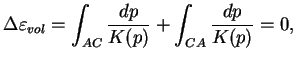suivant: Hyperélasticité non-linéaire isotrope
monter: Discussion sur la réversibilité
précédent: est constant
Table des matières
Dans ce cas, le coefficient de Poisson a pour expression en
fonction de la pression moyenne :
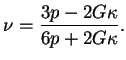 |
(3.20.23) |
Ainsi, l'équation (3.4.20) devient :
et l'équation (3.4.21) devient :
 |
(3.20.24) |
En posant
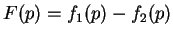 qui en A et en C est nulle,
(3.4.24) devient :
qui en A et en C est nulle,
(3.4.24) devient :
 |
(3.20.25) |
En remplaçant  par (3.4.23), (3.4.25)
devient :
par (3.4.23), (3.4.25)
devient :
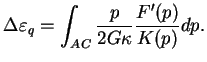 |
(3.20.26) |
Or 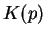 a pour expression :
a pour expression :
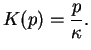 |
(3.20.27) |
Soit, en mettant (3.4.27) dans (3.4.26) on obtient :
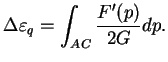 |
(3.20.28) |
Puisque le module de cisaillement  ne dépend pas de la pression
moyenne
ne dépend pas de la pression
moyenne 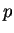 , l'intégrale se résume à une intégrale sur la fonction
, l'intégrale se résume à une intégrale sur la fonction
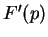 entre les points
entre les points 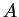 et
et 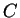 . Or, en ces points, la
fonction
. Or, en ces points, la
fonction 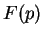 est nulle. Ainsi, la déformation déviatoire est
nulle pour un cycle de chargement en contrainte. Le modèle est
donc conservatif. Cependant, ce modèle peut conduire à des valeurs
du coefficient de Poisson négatives, ce qui n'est pas physiquement
raisonnable.
L'alternative qui vient d'être explorée ne donne pas la possibilité
d'obtenir de solution pour modéliser le comportement élastique non-linéaire. La
résolution de ce problème passe par un autre cheminement. Par
exemple, déterminer un potentiel élastique dont dérive la loi de
comportement. C'est l'objet de la section suivante.
est nulle. Ainsi, la déformation déviatoire est
nulle pour un cycle de chargement en contrainte. Le modèle est
donc conservatif. Cependant, ce modèle peut conduire à des valeurs
du coefficient de Poisson négatives, ce qui n'est pas physiquement
raisonnable.
L'alternative qui vient d'être explorée ne donne pas la possibilité
d'obtenir de solution pour modéliser le comportement élastique non-linéaire. La
résolution de ce problème passe par un autre cheminement. Par
exemple, déterminer un potentiel élastique dont dérive la loi de
comportement. C'est l'objet de la section suivante.




suivant: Hyperélasticité non-linéaire isotrope
monter: Discussion sur la réversibilité
précédent: est constant
Table des matières
FRACHON Arnaud
2002-11-12