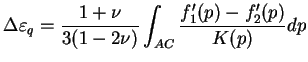$\nu$ est constant

Dans ce cas, le module de cisaillement est variable et a pour expression en fonction de la pression moyenne :

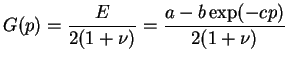$$G(p)=\frac{E}{2(1+ \nu)}=\frac{a-b \exp(-c p)}{2(1+ \nu)}$$ (3.20.22)

Dans ce cas, l'équation (3.4.20) devient :

$$\Delta \varepsilon_{vol} = \int_{ABC} \frac{dp}{K(p)} + \int_{CDA} \frac{dp}{K(p)} = \int_{AC} \frac{dp}{K(p)} - \int_{CA} \frac{dp}{K(p)} =0 ,$$

et l'équation (3.4.21) devient :

$$\Delta \varepsilon_{q} = \frac{1+ \nu}{3(1-2\nu)} \int_{AC} \frac{f'_1(p)-f'_2(p)}{K(p)}dp$$

On voit très bien que dans ce cas, à la fin du cycle, il y a une déformation déviatoire résiduelle dans le cas général où les deux fonctions de charge et de décharge sont différentes. Ainsi, dans le cas où le module d'Young est variable, le module de cisaillement est variable et le coefficient de Poisson constant, on aboutit à un modèle non conservatif.