suivant: est constant
monter: Élasticité non-linéaire isotrope
précédent: Élasticité du modèle de
Table des matières
Le modèle élastique non-linéaire de CamClay doit, comme tout
modèle élastique, être une fonction bijective entre l'état de
contraintes et l'état de déformations élastiques. En d'autre
termes, à un état de contraintes ne correspond qu'un et un seul
état de déformations élastiques (compte tenu de la décomposition
de l'état de déformation). Nulle déformation inélastique ne doit
apparaître à la suite d'un cycle fermé3.1 de
chargement en contraintes. Dans le cadre de la partie élastique du
modèle de CamClay, Zytinski & al. [ZRNW78] ont mis
en lumière les restrictions nécessaires à ce modèle pour que
celui-ci soit conservatif (pas de dissipation d'énergie). Les
principales étapes de cette démonstration sont exposées dans cette
section.
La plupart des modèles proposés ont pour origine une extension de
l'élastoplasticité classique du comportement des métaux. Dans la
région élastique, il n'y a pas de dissipation d'énergie et la
réponse est conservative (la déformation dérive d'un potentiel).
Zytinski & al. [ZRNW78] se proposent de modéliser la
région élastique. Pour cela, ils considèrent la relation élastique
suivante :
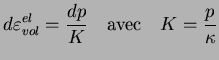 |
(3.20.13) |
Si on considère que le coefficient de Poisson est constant, il
vient que le module de cisaillement se déduit de la relation de
l'élasticité infinitésimale suivante :
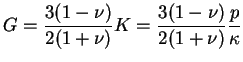 |
(3.20.14) |
Afin de voir si ces relations sont conservatives, on applique un
chemin de contraintes cycliques a un échantillon cylindrique. Le
chemin de contraintes est par exemple dans le plan p-q. La loi de
Hooke nous donne :
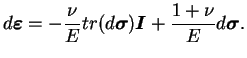 |
(3.20.15) |
Dans le cas d'une compression simple, la déformation volumique se
résume à
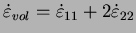 . D'où, en utilisant la relation
(3.4.15) on obteint :
. D'où, en utilisant la relation
(3.4.15) on obteint :
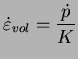 |
(3.20.16) |
Avec
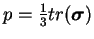 la pression isotrope.
De la même manière, on a la déformation déviatoire qui, dans le
cas d'une compression simple, a pour expression :
la pression isotrope.
De la même manière, on a la déformation déviatoire qui, dans le
cas d'une compression simple, a pour expression :
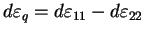 . En
utilisant le loi de Hooke (3.4.15), on obtient :
. En
utilisant le loi de Hooke (3.4.15), on obtient :
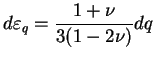 |
(3.20.17) |
où 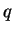 est la contrainte équivalente de Von Mises.
Le chargement cyclique que l'on applique au matériau illustré par
la figure 3.4.3 est le suivant :
est la contrainte équivalente de Von Mises.
Le chargement cyclique que l'on applique au matériau illustré par
la figure 3.4.3 est le suivant :
Figure 3.4.3:
chemins de contraintes en charge et en décharge
|
|
la mise en charge est effectuée sur un chemin ABC pour lequel on a
:
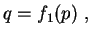 |
(3.20.18) |
et le retour s'effectue sur le chemin CDA pour lequel on a :
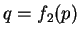 |
(3.20.19) |
il est à noter que les fonctions 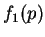 et
et 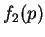 ont des
valeurs communes en A et C.
Si le modèle est conservatif, il n'y a pas de déformations
permanentes après un cycle de charge et de décharge. Soit, on doit
obtenir :
ont des
valeurs communes en A et C.
Si le modèle est conservatif, il n'y a pas de déformations
permanentes après un cycle de charge et de décharge. Soit, on doit
obtenir :
Maintenant, on va traiter deux cas où le module d'Young varie :
- le coefficient de Poisson est constant donc, le module de
cisaillement est variable
- le module de cisaillement est constant donc, le coefficient
de Poisson est variable.
Sous-sections




suivant: est constant
monter: Élasticité non-linéaire isotrope
précédent: Élasticité du modèle de
Table des matières
FRACHON Arnaud
2002-11-12