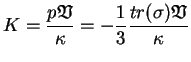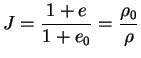suivant: Discussion sur la réversibilité
monter: Élasticité non-linéaire isotrope
précédent: Modèle de Lade
Table des matières
Le modèle de comportement de CamClay propose un modèle
élasto-plastique dont l'élasticité est non-linéaire.
L'expression tensorielle de cette élasticité est donnée par
l'équation 3.4.3 (
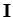 est le tenseur unité
d'ordre 2 et
est le tenseur unité
d'ordre 2 et
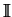 est le tenseur unité d'ordre 4)
exprimée par Callari & al.[CAS98] :
est le tenseur unité d'ordre 4)
exprimée par Callari & al.[CAS98] :
![$\displaystyle \dot{\sigma}=\left[ K \mathbf{I} \otimes \mathbf{I} + 2 \mu
\le...
...c{1}{3} \mathbf{I} \otimes \mathbf{I}
\right) \right] : \dot{\varepsilon ^e}$](img230.png) |
(3.20.3) |
où K est le module de dilatation volumique et 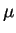 est le module
de cisaillement. De plus, le module K dépend de la pression
isotrope p(
est le module
de cisaillement. De plus, le module K dépend de la pression
isotrope p(
 ) de la façon suivante :
) de la façon suivante :
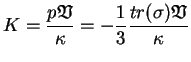 |
(3.20.4) |
où
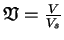 est le volume spécifique et
est le volume spécifique et
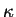 est un paramètre matériau.
Cette loi étant issue de la géomécanique, la déformation volumique
est exprimée en fonction de l'indice des vides
est un paramètre matériau.
Cette loi étant issue de la géomécanique, la déformation volumique
est exprimée en fonction de l'indice des vides 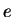 .
.
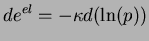 |
(3.20.5) |
L'équation (3.4.5) donne une relation bijective entre les
quantités volumiques sans faire apparaître de cohésion (pression
isotrope résistant à la traction isotrope). Pour avoir cette
résistance à la traction, il suffit de déplacer l'origine des
pressions comme présenté dans l'équation (3.4.6):
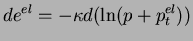 |
(3.20.6) |
Où  représente la résistance à la traction isotrope (la
cohésion). Une telle relation peut être reprise pour la
métallurgie des poudres en remplaçant l'indice des vides par la
masse volumique. Ainsi, il en résulte que l'équation (3.4.6)
devient :
représente la résistance à la traction isotrope (la
cohésion). Une telle relation peut être reprise pour la
métallurgie des poudres en remplaçant l'indice des vides par la
masse volumique. Ainsi, il en résulte que l'équation (3.4.6)
devient :
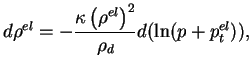 |
(3.20.7) |
où
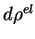 représente l'incrément de masse volumique dû au
mécanisme réversible. Cet incrément s'efface lorsque la contrainte
est nulle.
Il peut être montré que, si la compressibilité du squelette est
négligée, la variation volumique du matériau n'est due qu'à la
variation du volume des vides :
représente l'incrément de masse volumique dû au
mécanisme réversible. Cet incrément s'efface lorsque la contrainte
est nulle.
Il peut être montré que, si la compressibilité du squelette est
négligée, la variation volumique du matériau n'est due qu'à la
variation du volume des vides :
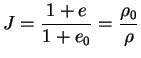 |
(3.20.8) |
où 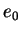 est la valeur initiale de l'indice des vides et
est la valeur initiale de l'indice des vides et 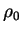 est la masse volumique initiale. L'évolution de
est la masse volumique initiale. L'évolution de 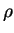 décrit
l'évolution de la déformation volumique inversement au jacobien
décrit
l'évolution de la déformation volumique inversement au jacobien
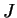 .
En considérant la décomposition de la déformation volumique en une
partie élastique et une partie plastique, on a :
.
En considérant la décomposition de la déformation volumique en une
partie élastique et une partie plastique, on a :
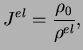 |
(3.20.9) |
où 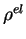 est la masse volumique due à l'élasticité depuis
est la masse volumique due à l'élasticité depuis
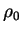 .
En plaçant la relation (3.4.7) dans la relation (3.4.9)
et en intégrant entre l'instant initial et l'instant courant, on
obtient :
.
En plaçant la relation (3.4.7) dans la relation (3.4.9)
et en intégrant entre l'instant initial et l'instant courant, on
obtient :
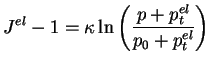 |
(3.20.10) |
où 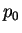 est la contrainte isotrope initiale donnée pas les
conditions initiales.
La relation (3.4.10) a pour réciproque :
est la contrainte isotrope initiale donnée pas les
conditions initiales.
La relation (3.4.10) a pour réciproque :
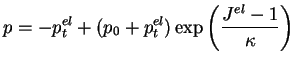 |
(3.20.11) |
Le comportement déviatorique de cette élasticité peut être
linéaire on non-linéaire. Dans l'état actuel de nos connaissances,
on commencera pas une réponse élastique déviatoire linéaire
définie par le module de cisaillement G.
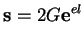 |
(3.20.12) |
où
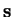 est le tenseur des contraintes déviatoires, et
est le tenseur des contraintes déviatoires, et
 est le tenseur des déformations déviatoires.
Ce type de non-linéarité est intéressant du fait qu'il est issu de
la mécanique des milieux pulvérulents et plus précisément, il
modélise le comportement d'un matériau dont la morphologie des
particules est semblable à la poudre métallique déformée
plastiquement. Par contre, cette morphologie n'est pas prise en
compte au niveau de la loi qui est isotrope. Part ailleurs, le
fait que le cisaillement soit constant (3.4.12) ne convient pas
pour la métallurgie des poudres et plus particulièrement pour les
poudres de fer.
est le tenseur des déformations déviatoires.
Ce type de non-linéarité est intéressant du fait qu'il est issu de
la mécanique des milieux pulvérulents et plus précisément, il
modélise le comportement d'un matériau dont la morphologie des
particules est semblable à la poudre métallique déformée
plastiquement. Par contre, cette morphologie n'est pas prise en
compte au niveau de la loi qui est isotrope. Part ailleurs, le
fait que le cisaillement soit constant (3.4.12) ne convient pas
pour la métallurgie des poudres et plus particulièrement pour les
poudres de fer.




suivant: Discussion sur la réversibilité
monter: Élasticité non-linéaire isotrope
précédent: Modèle de Lade
Table des matières
FRACHON Arnaud
2002-11-12
![$\displaystyle \dot{\sigma}=\left[ K \mathbf{I} \otimes \mathbf{I} + 2 \mu
\le...
...c{1}{3} \mathbf{I} \otimes \mathbf{I}
\right) \right] : \dot{\varepsilon ^e}$](img230.png)