suivant: Cadre thermodynamique
monter: Définitions et résultats cinématiques
précédent: Point de vue Lagrangien
Table des matières
On écrit
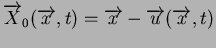 . Le
vecteur
. Le
vecteur
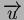 dépend des coordonnées spatiales.
Pour ce rappel, le point de vue adopté est le cas d'une
représentation Lagrangienne. Il est considéré la configuration
initiale d'un domaine à un instant
dépend des coordonnées spatiales.
Pour ce rappel, le point de vue adopté est le cas d'une
représentation Lagrangienne. Il est considéré la configuration
initiale d'un domaine à un instant 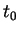 et sa configuration
courante à un instant
et sa configuration
courante à un instant 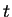 . La position initiale d'un point du
domaine est notée :
. La position initiale d'un point du
domaine est notée :
 . Les composantes de ce
vecteur seront notées avec un indice 0 . La position courante de
ce même point est notée :
. Les composantes de ce
vecteur seront notées avec un indice 0 . La position courante de
ce même point est notée :
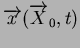 .
La configuration courante est liée à la configuration initiale au
travers du tenseur gradient des transformations
.
La configuration courante est liée à la configuration initiale au
travers du tenseur gradient des transformations
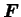 et définie par :
et définie par :
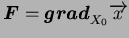 |
(4.27.1) |
De ce tenseur, il en découle plusieurs combinaisons donnant lieu à
des tenseurs exprimant une partie de la transformation. Cette
partie correspond à la déformation du domaine considéré. Parmi les
combinaisons il y a :
- le tenseur des dilatations de Cauchy
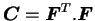
- le tenseur des déformations de GREEN

Le tenseur gradient de la transformation peut être décomposé comme
suit (décomposition canonique) :
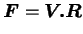 |
(4.27.2) |
Le tenseur
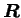 représentant la rotation d'un corps
rigide, ce tenseur est orthogonal, donc :
représentant la rotation d'un corps
rigide, ce tenseur est orthogonal, donc :
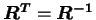 . Ainsi, on peut calculer le tenseur
. Ainsi, on peut calculer le tenseur
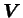 (tenseur des déformations à gauche) de la façon
suivante :
(tenseur des déformations à gauche) de la façon
suivante :
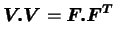 |
(4.27.3) |
Ainsi :
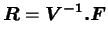 |
(4.27.4) |
On note 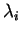 les valeurs principales du tenseur
les valeurs principales du tenseur
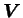 , et
, et
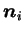 les vecteurs principaux
associés. Dans ce repère principal sont définis :
Le tenseur des déformations nominales (déformation de BIOT)
les vecteurs principaux
associés. Dans ce repère principal sont définis :
Le tenseur des déformations nominales (déformation de BIOT)
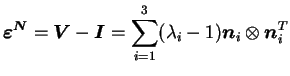 |
(4.27.5) |
Le tenseur des déformations logarithmiques ou des déformations
naturelles
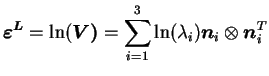 |
(4.27.6) |
C'est cette définition de la déformation qui est utilisée dans les
travaux présentés dans ce mémoire.
La transformation des volumes est interprété par le Jacobien
défini par :
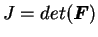 |
(4.27.7) |
L'ensemble des combinaisons de
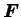 sont des variables
extensives. Il est également possible de définir parmi ces
variables, le tenseur gradient des vitesses
sont des variables
extensives. Il est également possible de définir parmi ces
variables, le tenseur gradient des vitesses
 :
dont la partie symétrique définit le tenseur taux de déformations
:
Chaque variable extensive possède un dual, la variable intensive.
Ainsi, le dual par rapport à l'énergie de déformations de
:
dont la partie symétrique définit le tenseur taux de déformations
:
Chaque variable extensive possède un dual, la variable intensive.
Ainsi, le dual par rapport à l'énergie de déformations de
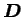 dans le repère initial est le tenseur des
contraintes de Kirchoff
dans le repère initial est le tenseur des
contraintes de Kirchoff
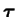 défini par :
où
défini par :
où
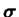 est la contrainte de Cauchy. Il est à
noter que le tenseur de Kirchoff est symétrique.
La combinaison des variables extensives et des variables
intensives permet de déterminer le travail (
est la contrainte de Cauchy. Il est à
noter que le tenseur de Kirchoff est symétrique.
La combinaison des variables extensives et des variables
intensives permet de déterminer le travail (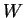 ) sur le domaine
considéré :
) sur le domaine
considéré :
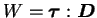 . Ceci est pris
en compte dans ce qui suit.
. Ceci est pris
en compte dans ce qui suit.




suivant: Cadre thermodynamique
monter: Définitions et résultats cinématiques
précédent: Point de vue Lagrangien
Table des matières
FRACHON Arnaud
2002-11-12