



suivant: Application à la plasticité
monter: Modélisation élasto-plastique
précédent: Point de vue Eulérien
Table des matières
Dans ce chapitre, sont présentées des lois de comportement.
Celles-ci étant décrites dans le cadre de la mécanique des milieux
continus, elles doivent vérifier les principes de la
thermodynamique.
Afin de poser le cadre thermodynamique, les hypothèses suivantes
sont posées :
- l'état thermodynamique du corps est décrit par un certain
nombre de variables d'état indépendantes (
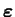 ) et de variables internes (
) et de variables internes (
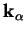 scalaires ou tensorielles). Les variables d'état suffisent à
décrire l'évolution du milieu durant un processus thermodynamique
réversible (comportement élastique). Par contre, les variables
internes - prises constantes dans un processus réversible -
décrivent la dissipation interne du matériau. Leurs évolutions
dans le temps sont commandées par les variables d'état.
scalaires ou tensorielles). Les variables d'état suffisent à
décrire l'évolution du milieu durant un processus thermodynamique
réversible (comportement élastique). Par contre, les variables
internes - prises constantes dans un processus réversible -
décrivent la dissipation interne du matériau. Leurs évolutions
dans le temps sont commandées par les variables d'état.
- l'état thermodynamique d'une particule est déterminé par
l'histoire des états thermodynamiques de cette particule
(principe de causalité et principe de localisation spatiale).
- il existe une énergie libre
 (
( est la température, U
est l'énergie interne et S est l'entropie).
est la température, U
est l'énergie interne et S est l'entropie).
Le premier principe de la thermodynamique indique qu'il y a
conservation de l'énergie au cours d'une transformation si l'on
inclut la chaleur ( ) échangée entre le système et son
environnement :
Dans les cas qui vont être considérés, la température est supposée
homogène dans le domaine et constante au cours du temps. En
ignorant les puissances non-mécaniques et l'énergie cinétique, le
second principe de la thermodynamique conduit à la forme réduite
de l'inégalité de dissipation :
) échangée entre le système et son
environnement :
Dans les cas qui vont être considérés, la température est supposée
homogène dans le domaine et constante au cours du temps. En
ignorant les puissances non-mécaniques et l'énergie cinétique, le
second principe de la thermodynamique conduit à la forme réduite
de l'inégalité de dissipation :
 |
(4.27.8) |
Dans le cas d'une transformation réversible, l'inégalité
(4.3.8) se transforme en une égalité signifiant la
non-dissipation.
Si l'on note
 dans le repère final, on en déduit :
quelque soit
dans le repère final, on en déduit :
quelque soit
 .
En admettant qu'il existe, au voisinage de tout état, un domaine
élastique pour lequel la microstructure (variables
.
En admettant qu'il existe, au voisinage de tout état, un domaine
élastique pour lequel la microstructure (variables
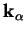 ) est "figée", alors il est possible
d'envisager des transformations telles que :
Pour retrouver l'élastoplasticité classique, il est supposé une
décomposition de la déformation (
) est "figée", alors il est possible
d'envisager des transformations telles que :
Pour retrouver l'élastoplasticité classique, il est supposé une
décomposition de la déformation (
 ). De
plus, les variables internes
). De
plus, les variables internes
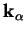 sont :
sont :
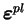 et X (tenseur d'ordre 0, 1
ou 2). Ainsi, pour l'énergie libre, on a :
car il y a une décomposition de la déformation. Cette dépendance
implique :
Soit, l'état de contraintes est fonction des variables internes et
de la déformation élastique. En outre, la condition de dissipation
s'écrit :
Lorsque le comportement est élastique, la dissipation est nulle.
La dissipation n'est donc due qu'au comportement plastique. C'est
ce comportement qui est étudié.
et X (tenseur d'ordre 0, 1
ou 2). Ainsi, pour l'énergie libre, on a :
car il y a une décomposition de la déformation. Cette dépendance
implique :
Soit, l'état de contraintes est fonction des variables internes et
de la déformation élastique. En outre, la condition de dissipation
s'écrit :
Lorsque le comportement est élastique, la dissipation est nulle.
La dissipation n'est donc due qu'au comportement plastique. C'est
ce comportement qui est étudié.




suivant: Application à la plasticité
monter: Modélisation élasto-plastique
précédent: Point de vue Eulérien
Table des matières
FRACHON Arnaud
2002-11-12



