



suivant: Modèles plastiques isotropes
monter: Application à la plasticité
précédent: Application à la plasticité
Table des matières
Lors de la décharge, on a :
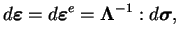 |
(4.27.14) |
où
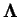 est le tenseur élastique.
Pour la charge plastique, on a :
est le tenseur élastique.
Pour la charge plastique, on a :
 |
(4.27.15) |
où
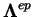 est le tenseur des raideurs
élasto-plastiques.
Cela peut s'écrire également :
est le tenseur des raideurs
élasto-plastiques.
Cela peut s'écrire également :
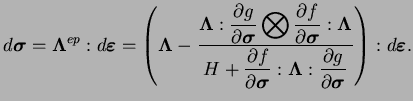 |
(4.27.16) |
Ces formules s'appliquent en des points réguliers de la surface de
charge et du potentiel plastique.
Le module de plasticité est défini de la manière suivante :
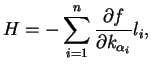 |
(4.27.17) |
où 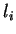 sont les fonctions constitutives de la relation linéaire
entre paramètres d'écrouissage et l'état de contraintes
(
sont les fonctions constitutives de la relation linéaire
entre paramètres d'écrouissage et l'état de contraintes
(
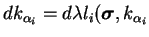 )).
Cette théorie peut être appliquée tant au cas isotrope qu'au cas
anisotrope. La distinction entre ces cas est faite dans ce qui
suit.
)).
Cette théorie peut être appliquée tant au cas isotrope qu'au cas
anisotrope. La distinction entre ces cas est faite dans ce qui
suit.




suivant: Modèles plastiques isotropes
monter: Application à la plasticité
précédent: Application à la plasticité
Table des matières
FRACHON Arnaud
2002-11-12