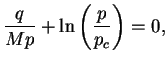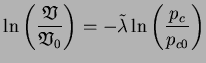suivant: Modèle modifié non-cohésif
monter: Les modèles de CamClay
précédent: Les modèles de CamClay
Table des matières
Le modèle initialement proposé par Schoefield &
al.[SW68] propose comme surface de charges, l'équation
4.4.1.
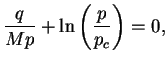 |
(4.28.1) |
où M est une constante du matériau. Cette surface de charges est
paramétrée par 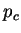 . La loi d'écrouissage relie ce paramètre
. La loi d'écrouissage relie ce paramètre
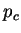 à la variable d'écrouissage
à la variable d'écrouissage
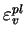 (la
déformation volumique plastique). Cette relation est donnée dans
l'équation (4.4.2).
(la
déformation volumique plastique). Cette relation est donnée dans
l'équation (4.4.2).
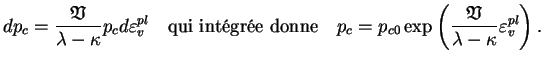 |
(4.28.2) |
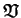 ,
, 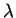 ,
, 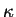 et
et 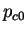 sont aussi des
constantes du matériau. Or, cette expression n'est valable que
dans le cadre des déformations infinitésimales. Cette formulation
rend possible des valeurs du volume spécifique (
sont aussi des
constantes du matériau. Or, cette expression n'est valable que
dans le cadre des déformations infinitésimales. Cette formulation
rend possible des valeurs du volume spécifique (
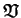 )
négatives. Une alternative est alors proposée dans le cas des
grandes déformations :
Les états critiques correspondent à l'état le plus déviatoire de
la surface de charges et sont décrits par l'équation
4.4.3
)
négatives. Une alternative est alors proposée dans le cas des
grandes déformations :
Les états critiques correspondent à l'état le plus déviatoire de
la surface de charges et sont décrits par l'équation
4.4.3
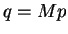 |
(4.28.3) |
La surface de charges est présentée dans un plan p-q sur la figure
4.4.1.
Figure 4.4.1:
Représentation du critère de CamClay initial dans un plan p-q
|
|
Le modèle ainsi établi décrit la densification lorsque l'état de
contraintes est en-dessous de la droite de l'état critique.
Lorsque l'état de contraintes est au-dessus de cette droite, le
modèle décrit la dilatance. Il est à noter que sur l'axe de
contrainte isotrope p, la surface présente une indétermination
pour la direction d'écoulement.




suivant: Modèle modifié non-cohésif
monter: Les modèles de CamClay
précédent: Les modèles de CamClay
Table des matières
FRACHON Arnaud
2002-11-12