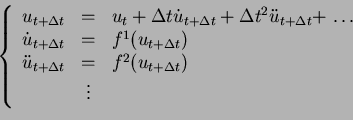suivant: Abaqus/Standard
monter: Schémas implicites
précédent: Schémas implicites
Table des matières
Le principe de ce schéma consiste à résoudre l'équation
d'équilibre à l'instant
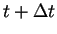 :
:
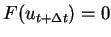 . Or, la solution
. Or, la solution
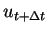 est contenue dans
l'équation à résoudre. La résolution est donc déterminée par
récurrence sur l'incrément de temps.
est contenue dans
l'équation à résoudre. La résolution est donc déterminée par
récurrence sur l'incrément de temps.
Figure 5.2.1:
Illustration du schéma implicite d'intégration au cours
du temps
|
|
La figure 5.2.1 illustre le principe des différences
finies implicites.
La valeur nodale
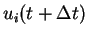 est calculée à partir de la
valeur
est calculée à partir de la
valeur 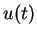 et de ces dérivées en
et de ces dérivées en
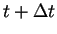 . L'indice
représente les différentes itérations qui mènent à la valeur
nodale. C'est une résolution d'un système d'équations couplées à
chaque pas de temps comme suit.
L'un des avantages majeurs de ce type de résolution est que ce schéma
est inconditionnellement stable i.e. la convergence n'est
pas soumise à des restrictions numériques. Cependant, la
convergence peut être longue, impliquant de longs temps de calculs
pour des problèmes quelques peu compliqués.
. L'indice
représente les différentes itérations qui mènent à la valeur
nodale. C'est une résolution d'un système d'équations couplées à
chaque pas de temps comme suit.
L'un des avantages majeurs de ce type de résolution est que ce schéma
est inconditionnellement stable i.e. la convergence n'est
pas soumise à des restrictions numériques. Cependant, la
convergence peut être longue, impliquant de longs temps de calculs
pour des problèmes quelques peu compliqués.
FRACHON Arnaud
2002-11-12