



suivant: Schémas explicite
monter: Schémas implicites
précédent: Principe général
Table des matières
Généralement, c'est la méthode de Newton qui est utilisée pour
résoudre les problèmes non-linéaires. La base du formalisme de
cette méthode est la suivante. Considérons qu'après i
itérations sur l'incrément de temps, l'approximation de la solution
est 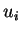 . La différence entre la solution exacte et la solution
après i itérations est notée
. La différence entre la solution exacte et la solution
après i itérations est notée 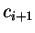 . La solution exacte
est donc donnée par
En écrivant
symboliquement le principe des travaux virtuels par une équation
implicite,
cela signifie l'équilibre par rapport à la
variable nodale considérée. Cette équation implicite peut être
développée en série de Taylor en
. La solution exacte
est donc donnée par
En écrivant
symboliquement le principe des travaux virtuels par une équation
implicite,
cela signifie l'équilibre par rapport à la
variable nodale considérée. Cette équation implicite peut être
développée en série de Taylor en 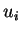 , ce qui donne :
, ce qui donne :
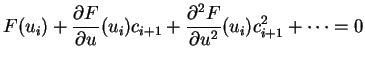 |
(5.32.3) |
Si l'approximation 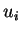 est proche de la solution, alors
est proche de la solution, alors
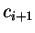 est petit et l'équation (5.2.3) peut être réduite
à ces deux premiers termes donnant ainsi :
est petit et l'équation (5.2.3) peut être réduite
à ces deux premiers termes donnant ainsi :
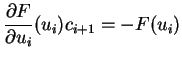 |
(5.32.4) |
Cette équation (5.2.4) permet de déterminer 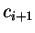 pour
calculer l'approximation suivante
pour
calculer l'approximation suivante 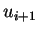 par
par
Figure 5.2.2:
Illustration de la méthode de Newton
|
|
La figure 5.2.2 illustre la méthode de Newton dont le but
est de déterminer 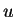 tel que
tel que 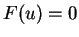 . Sur cette figure, on
observe que la valeur nodale de l'incrément suivant utilise la
matrice jacobienne comme une pente, en partant de la valeur
courante.
La convergence de cette méthode est quadratique, donc rapide.
Cependant, la matrice jacobienne (
. Sur cette figure, on
observe que la valeur nodale de l'incrément suivant utilise la
matrice jacobienne comme une pente, en partant de la valeur
courante.
La convergence de cette méthode est quadratique, donc rapide.
Cependant, la matrice jacobienne (
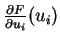 ) peut présenter des problèmes d'existence et de
singularité. Auquel cas, l'équation (5.2.4) est insoluble.
) peut présenter des problèmes d'existence et de
singularité. Auquel cas, l'équation (5.2.4) est insoluble.




suivant: Schémas explicite
monter: Schémas implicites
précédent: Principe général
Table des matières
FRACHON Arnaud
2002-11-12