



suivant: Le frottement
monter: Interactions entre surfaces
précédent: Interactions entre surfaces
Table des matières
Dans la version explicite du code Abaqus, le contact est modélisé
en utilisant une surface maître et une surface esclave. Les n uds de la surface esclave ne peuvent et ne doivent pas pénétrer la
surface maître.
Dans un premier temps, les vecteurs normaux normés sont calculés
pour chaque n
uds de la surface esclave ne peuvent et ne doivent pas pénétrer la
surface maître.
Dans un premier temps, les vecteurs normaux normés sont calculés
pour chaque n ud de la surface maître. Ces vecteurs sont nommés
ud de la surface maître. Ces vecteurs sont nommés
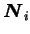 où l'indice
où l'indice 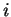 indique le numéro du n
indique le numéro du n ud.
De plus, des vecteurs normaux normés sont calculés pour chaque
segment (en 2D) de la surface maître. Ces vecteurs sont notés
ud.
De plus, des vecteurs normaux normés sont calculés pour chaque
segment (en 2D) de la surface maître. Ces vecteurs sont notés
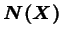 où
où
 représente un point de la
surface maître.
représente un point de la
surface maître.
Figure 5.4.1:
Contact entre une surface maître et une surface esclave
|
|
Un point d'ancrage
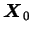 est calculé pour chaque n
est calculé pour chaque n ud esclave tel que le vecteur construit par le n
ud esclave tel que le vecteur construit par le n ud esclave et
ce point d'ancrage coïncide avec le vecteur normal
ud esclave et
ce point d'ancrage coïncide avec le vecteur normal
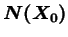 ainsi que le montre la figure 5.4.1.
où
ainsi que le montre la figure 5.4.1.
où 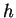 est la mesure de la proximité entre la surface maître
est la mesure de la proximité entre la surface maître
 paramétrée par
paramétrée par 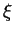 et le n
et le n ud esclave
ud esclave
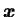 . Pour un n
. Pour un n ud esclave donné, si
ud esclave donné, si 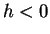 alors il
n'y a pas de contact. Par contre, si
alors il
n'y a pas de contact. Par contre, si
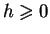 , les surfaces
sont en contact. La contrainte de contact est exprimée par
, les surfaces
sont en contact. La contrainte de contact est exprimée par 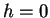 .
Par défaut, c'est un algorithme de contact cinématique qui est
appliqué. Cet algorithme est décrit en six points dans le manuel
de référence au code de calcul [HKS98b].
.
Par défaut, c'est un algorithme de contact cinématique qui est
appliqué. Cet algorithme est décrit en six points dans le manuel
de référence au code de calcul [HKS98b].
- Actualisation de la configuration sans tenir compte des
contacts.
- Test sur l'existence de n
 uds esclaves qui ont pénétrés
la surface maître.
uds esclaves qui ont pénétrés
la surface maître.
- La profondeur de pénétration (
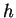 ), la masse des n
), la masse des n uds
et l'incrément de temps sont utilisés pour déterminer la force
nécessaire pour éviter cette pénétration. Cette force est
interprétée comme étant celle qui a été appliquée au cours de
cet incrément de temps pour que le n
uds
et l'incrément de temps sont utilisés pour déterminer la force
nécessaire pour éviter cette pénétration. Cette force est
interprétée comme étant celle qui a été appliquée au cours de
cet incrément de temps pour que le n ud esclave pénètre la
surface maître.
ud esclave pénètre la
surface maître.
- L'ensemble de ces forces résistives est distribué aux
n
 uds de la surface maître.
uds de la surface maître.
- La masse de chaque n
 ud esclave en contact est
distribuée aux n
ud esclave en contact est
distribuée aux n uds de la surface maître et ajoutée à leur
propre masse pour évaluer la masse inertielle totale de
l'interface.
uds de la surface maître et ajoutée à leur
propre masse pour évaluer la masse inertielle totale de
l'interface.
- Le code utilise les forces et les nouvelles masses pour
déterminer une accélération de correction pour les n
 uds de
la surface maître. Ces accélérations de correction sont
utilisées pour obtenir une configuration correcte dans laquelle
la contrainte de contact est respectée.
uds de
la surface maître. Ces accélérations de correction sont
utilisées pour obtenir une configuration correcte dans laquelle
la contrainte de contact est respectée.
Il est possible que la surface maître pénètre la surface esclave.
Il reste que ce type d'algorithme est plus rigoureux que
l'algorithme de contact par pénalisation.




suivant: Le frottement
monter: Interactions entre surfaces
précédent: Interactions entre surfaces
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=8cm]{contact.eps}](img706.png)