



suivant: Intégration de lois élasto-plastiques
monter: Interactions entre surfaces
précédent: Le contact
Table des matières
Lorsque le contact est établi entre deux surfaces, qu'advient il
pour un mouvement relatif tangent entre ces deux surfaces ? Il
s'avère que l'interaction est énergiquement dissipatrice.
Classiquement, le comportement tangentiel à l'interface est
modélisé par le frottement de Coulomb. Ce modèle admet une
contrainte de cisaillement critique (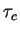 ) en dessous de
laquelle le mouvement relatif entre deux surfaces n'est pas
autorisé ainsi que l'illustre la figure 5.4.2.
) en dessous de
laquelle le mouvement relatif entre deux surfaces n'est pas
autorisé ainsi que l'illustre la figure 5.4.2.
Figure 5.4.2:
Évolution de la distorsion 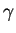 en fonction de la
contrainte de cisaillement
en fonction de la
contrainte de cisaillement 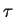
|
|
Cette contrainte limite est fonction de la contrainte normale
appliquée à l'interface. Dans le cas du modèle de Coulomb, la
relation entre la contrainte normale 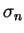 et la contrainte
tangentielle
et la contrainte
tangentielle 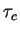 est linéaire et donnée par l'équation
(5.4.1).
est linéaire et donnée par l'équation
(5.4.1).
 |
(5.34.1) |
Ces contraintes sont illustrées sur la figure 5.4.3.
Figure 5.4.3:
Décomposition de l'état de contrainte à l'interface
en une contrainte normale 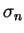 et une contrainte tangentielle
et une contrainte tangentielle
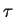
|
|
Numériquement, il faut évaluer la matrice de rigidité pour
l'interface des éléments. La détermination de cette matrice
nécessite la linéarisation des équations qui régissent le problème
du contact frottant. Il résulte de cette opération une dissymétrie
de la matrice constitutive. Afin de conserver la symétrie des
matrices, les termes hors diagonales, représentant le couplage
entre les contraintes normales et tangentielles, sont négligés.
Ainsi, le problème du contact est simplifié en une décomposition
d'un pur contact dans la direction normale et un frottement
résistant dans la direction tangentielle.




suivant: Intégration de lois élasto-plastiques
monter: Interactions entre surfaces
précédent: Le contact
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=8cm]{coulomb.eps}](img716.png)
![\includegraphics[width=8cm]{frotte.eps}](img718.png)