



suivant: Lois de comportement utilisées
monter: Intégration de lois élasto-plastiques
précédent: Intégration de lois élasto-plastiques
Table des matières
Il y a plusieurs méthodes d'intégration qui sont notamment
exposées par Macari & al. [MWA97]. Ces auteurs
exposent des méthodes implicites (Backward Euler, generalized
midpoint rule and generalized trapezoïdal rule) et
explicites(Foward Euler et Vermeer scheme).
La forme générale des équations constitutives des matériaux
élasto-plastiques est donnée par :
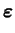 |
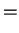 |
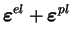 |
(5.35.1) |
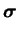 |
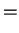 |
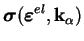 |
(5.35.2) |
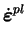 |
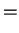 |
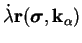 |
(5.35.3) |
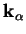 |
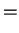 |
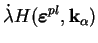 |
(5.35.4) |
L'équation (5.5.1) exprime la décomposition de la
déformation totale en une partie élastique et une partie
plastique. L'équation (5.5.2) est la réponse élastique du
matériau. L'équation (5.5.3) donne l'écoulement plastique
non-associé et l'équation (5.5.4) exprime l'évolution des
paramètres d'écrouissage. Le paramètre
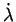 est le
multiplicateur de Lagrange ou multiplicateur plastique. Le tenseur
r est la direction de l'écoulement plastique. C'est la
normale au potentiel plastique. Le paramètre
est le
multiplicateur de Lagrange ou multiplicateur plastique. Le tenseur
r est la direction de l'écoulement plastique. C'est la
normale au potentiel plastique. Le paramètre
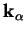 est une variable d'écrouissage et H est le module plastique. Pour
la suite, on aura besoin de la matrice élastique tangente
est une variable d'écrouissage et H est le module plastique. Pour
la suite, on aura besoin de la matrice élastique tangente
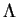 (d'ordre 4). Le multiplicateur plastique
(d'ordre 4). Le multiplicateur plastique
 est déterminé à l'aide de la charge-décharge du critère de
plasticité F. Ceci peut être exprimé par :
est déterminé à l'aide de la charge-décharge du critère de
plasticité F. Ceci peut être exprimé par :
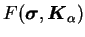 |
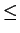 |
0 |
(5.35.5) |
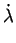 |
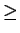 |
0 |
(5.35.6) |
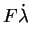 |
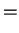 |
0 |
(5.35.7) |
Le critère est donné par l'inéquation (5.5.5) qui est
supposé convexe. Ce critère délimite le domaine élastique. La
condition de consistance plastique peut être exprimée par
l'inéquation (5.5.6). Au cours de toute
sollicitation, l'ensemble des équations (5.5.5),
(5.5.6) et (5.5.7) doit être vérifié.
Dans le cas où 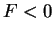 , il est nécessaire d'avoir
, il est nécessaire d'avoir
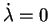 pour vérifier l'équation (5.5.7). On obtient alors le
comportement élastique. Dans les autres cas, l'écoulement
plastique est caractérisé par
pour vérifier l'équation (5.5.7). On obtient alors le
comportement élastique. Dans les autres cas, l'écoulement
plastique est caractérisé par
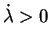 et par
conséquent,
et par
conséquent, 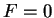 .
Dans le code de calcul par éléments finis que l'on a utilisé, on
impose la déformation. La déformation peut être vue comme une
fonction du temps. On peut ainsi réécrire les équations
(5.5.1), (5.5.2), (5.5.3) et (5.5.4)
de la façon suivante :
.
Dans le code de calcul par éléments finis que l'on a utilisé, on
impose la déformation. La déformation peut être vue comme une
fonction du temps. On peut ainsi réécrire les équations
(5.5.1), (5.5.2), (5.5.3) et (5.5.4)
de la façon suivante :
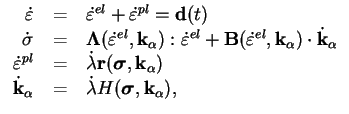 |
(5.35.8) |
où
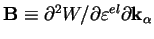 est une sorte de matrice de rigidité
mais qui tient compte de l'évolution des paramètres élastiques en
fonction des variables d'écrouissage. Les équations
(5.5.8) peuvent être décomposées en une partie
élastique et une partie plastique. La partie élastique des
équations (5.5.8) est donnée par :
est une sorte de matrice de rigidité
mais qui tient compte de l'évolution des paramètres élastiques en
fonction des variables d'écrouissage. Les équations
(5.5.8) peuvent être décomposées en une partie
élastique et une partie plastique. La partie élastique des
équations (5.5.8) est donnée par :
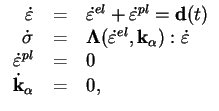 |
(5.35.9) |
et la partie plastique est donnée par :
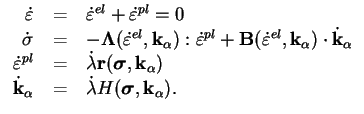 |
(5.35.10) |
En combinant les trois dernières équations de (5.5.10),
il résulte l'expression de l'incrément de relaxation de la
contrainte et l'incrément de la variable d'écrouissage, comme
donné par (5.5.11).
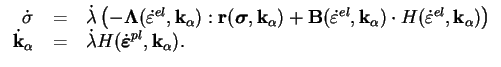 |
(5.35.11) |
Au début de l'incrément de déplacement, l'ensemble des variables
(
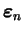 ,
,
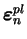 ,
,
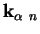 ,
,
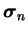 ) est connu. La
base du problème est de mettre à jour cet ensemble de champs de
variables pour obtenir l'ensemble des variables (
) est connu. La
base du problème est de mettre à jour cet ensemble de champs de
variables pour obtenir l'ensemble des variables (
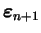 ,
,
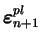 ,
,
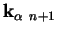 ,
,
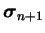 ). Au
début de l'incrément, la limite élastique est notée par
). Au
début de l'incrément, la limite élastique est notée par
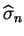 . Cette limite peut être exprimée comme une
partie de l'incrément de contrainte calculée à partir de la loi
élastique.
Finalement, le nouvel état de contrainte est donné par une
prédiction élastique diminuée d'une relaxation plastique. La
prédiction élastique est donnée par :
. Cette limite peut être exprimée comme une
partie de l'incrément de contrainte calculée à partir de la loi
élastique.
Finalement, le nouvel état de contrainte est donné par une
prédiction élastique diminuée d'une relaxation plastique. La
prédiction élastique est donnée par :
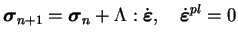 |
(5.35.12) |
La correction plastique est donnée par l'équation
(5.5.11). Il est proposé sur la figure
5.5.1 une illustration de la méthode
prédiction-correction.
Figure 5.5.1:
Illustration de la méthode prédiction élastique-correction
plastique
|
|
La prédiction est faite au travers de la loi élastique (incrément
de déformation supposé totalement élastique). Ensuite, la
correction plastique partitionne l'incrément de déformation totale
en une partie élastique et une partie plastique.
La différence des schémas d'intégration réside dans la façon de
discrétiser le problème. Les schémas peuvent être groupés en deux
catégories, celles qui utilisent une technique explicite et celles
qui utilisent une technique implicite. Les méthodes explicites
utilisent les variables en début d'incrément alors que les
méthodes implicites utilisent les variables en fin d'incrément.
Le choix de la technique d'intégration repose sur la
discrétisation du gradient de potentiel (
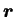 ).
).
- Méthodes explicites
- Forward Euler :
- Schéma de Vermeer :
- Méthodes implicites
- Méthode Backward Euler :
- Loi du point milieu généralisée :
- Loi trapézoïdale généralisée :
Dans le cas ou
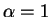 , alors les lois du point milieu
généralisé et trapézoïdale généralisé coïncident avec la méthode
de backward Euler. Cette méthode est particulièrement robuste et
elle est employée au travers de l'algorithme proposé par Ortiz et
Simo [OS86]. Le principe repose sur une mise à jour des
partitions des déformations, une prédiction élastique des
nouvelles contraintes puis une correction plastique. Il s'agit en
fait une correction de l'état de contraintes et des variables
d'écrouissage qui est répétée jusqu'à la convergence de la
solution. La solution idéale consiste en un état de contrainte
appartenant à la surface de charges écrouie. La solution numérique
n'est que voisine de la solution idéale dans un intervalle de
tolérance.
Les méthodes implicites présentent l'avantage d'être
inconditionnellement stable, contrairement aux méthodes explicites
qui nécessitent une condition de stabilité. De plus, les méthodes
implicites sont particulièrement robustes et offrent une
convergence rapide (moins de 20 itérations pour les testes
réalisés au cours de ces travaux).
, alors les lois du point milieu
généralisé et trapézoïdale généralisé coïncident avec la méthode
de backward Euler. Cette méthode est particulièrement robuste et
elle est employée au travers de l'algorithme proposé par Ortiz et
Simo [OS86]. Le principe repose sur une mise à jour des
partitions des déformations, une prédiction élastique des
nouvelles contraintes puis une correction plastique. Il s'agit en
fait une correction de l'état de contraintes et des variables
d'écrouissage qui est répétée jusqu'à la convergence de la
solution. La solution idéale consiste en un état de contrainte
appartenant à la surface de charges écrouie. La solution numérique
n'est que voisine de la solution idéale dans un intervalle de
tolérance.
Les méthodes implicites présentent l'avantage d'être
inconditionnellement stable, contrairement aux méthodes explicites
qui nécessitent une condition de stabilité. De plus, les méthodes
implicites sont particulièrement robustes et offrent une
convergence rapide (moins de 20 itérations pour les testes
réalisés au cours de ces travaux).




suivant: Lois de comportement utilisées
monter: Intégration de lois élasto-plastiques
précédent: Intégration de lois élasto-plastiques
Table des matières
FRACHON Arnaud
2002-11-12