



suivant: Les paramètres de Drucker-Prager/Cap
monter: Identification du comportement de
précédent: Identification du comportement de
Table des matières
Le modèle élastique utilisé pour ces simulations est le modèle de
Hooke. Ce modèle est caractérisé par deux paramètres intégrés au
code de calcul, le module d'Young (E) et le coefficient de Poisson
(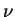 ). L'évolution de ces paramètres élastiques est donnée en
fonction de la déformation volumique plastique. La figure
6.2.1 donne l'évolution du module d'Young.
). L'évolution de ces paramètres élastiques est donnée en
fonction de la déformation volumique plastique. La figure
6.2.1 donne l'évolution du module d'Young.
Figure 6.2.1:
Évolution du module d'Young (E) en fonction de la
déformation volumique plastique
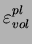 pour
une masse volumique initiale
pour
une masse volumique initiale

|
|
Le coefficient de Poisson est supposé constant tout au long de la
simulation, plus précisément 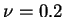 . Les mesures de ces deux
coefficients ont été réalisées par Pavier [PAV98] (pages
116-121) à l'aide du dispositif de compression triaxiale de
révolution. Des cycles de décharge-recharge ont été réalisés afin
de déterminer pour différentes densités les coefficients
caractérisant la partie élastique du comportement. Ces cycles
permettent une détermination correcte de la valeur moyenne du
module d'Young pour des états de confinement à contraintes
élevées. Par contre, la valeur du module d'Young fournie pour
chaque densité est une moyenne vis-à-vis du comportement réel de
l'échantillon. Le dispositif expérimental ne permet pas une mesure
continue et précise des déformations de l'état de confinement à
contraintes élevées à un état à contraintes pratiquement nulles.
Cependant, l'évolution moyenne de module de Young est donnée par
dans laquelle,
. Les mesures de ces deux
coefficients ont été réalisées par Pavier [PAV98] (pages
116-121) à l'aide du dispositif de compression triaxiale de
révolution. Des cycles de décharge-recharge ont été réalisés afin
de déterminer pour différentes densités les coefficients
caractérisant la partie élastique du comportement. Ces cycles
permettent une détermination correcte de la valeur moyenne du
module d'Young pour des états de confinement à contraintes
élevées. Par contre, la valeur du module d'Young fournie pour
chaque densité est une moyenne vis-à-vis du comportement réel de
l'échantillon. Le dispositif expérimental ne permet pas une mesure
continue et précise des déformations de l'état de confinement à
contraintes élevées à un état à contraintes pratiquement nulles.
Cependant, l'évolution moyenne de module de Young est donnée par
dans laquelle,
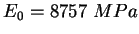 ,
,
 et
et
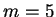 .
.




suivant: Les paramètres de Drucker-Prager/Cap
monter: Identification du comportement de
précédent: Identification du comportement de
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=12cm]{young9.eps}](img761.png)
![\includegraphics[width=12cm]{young9.eps}](img761.png)
