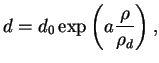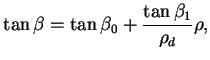suivant: Les paramètres du modèle
monter: Identification du comportement de
précédent: Les paramètres élastiques
Table des matières
La loi de Drucker-Prager/Cap est l'un des deux modèles de
comportement plastique utilisé pour réaliser les simulations des
pièces de validations. Ce modèle se caractérise par quatre
paramètres : la cohésion (d), l'angle de frottement interne
( ), l'excentricité de la surface du cap (R) et la pression
de consolidation (
), l'excentricité de la surface du cap (R) et la pression
de consolidation ( ), comme cela a été décrit au chapitre
4 dans la partie 4.4.2.
Les paramètres du mécanisme de Drucker-Prager (d et
), comme cela a été décrit au chapitre
4 dans la partie 4.4.2.
Les paramètres du mécanisme de Drucker-Prager (d et  ) sont
déterminés par des dispositifs faisant apparaître la rupture du
matériau. Parmi les dispositifs disponibles, les données peuvent
être issues de la compression uni-axiale, de la compression
diamétrale et de la traction simple. La figure 6.2.2
illustre la détermination des valeurs caractéristiques de ce
mécanisme par des essais de compression uniaxiale et de traction
uniaxiale.
) sont
déterminés par des dispositifs faisant apparaître la rupture du
matériau. Parmi les dispositifs disponibles, les données peuvent
être issues de la compression uni-axiale, de la compression
diamétrale et de la traction simple. La figure 6.2.2
illustre la détermination des valeurs caractéristiques de ce
mécanisme par des essais de compression uniaxiale et de traction
uniaxiale.
Figure 6.2.2:
Calage de la surface de Drucker/Prager par l'essai de
traction uniaxiale (à gauche) et l'essais de de compression uniaxiale
(à droite) dans le plan P-Q
|
|
Le résultat des mesures de contraintes à la rupture est présenté
sur la figure 6.2.3 à divers niveaux de masse volumique.
Figure 6.2.3:
Résultats de mesure pour caler les paramètres de la
droite de rupture avec contrainte de rupture en traction uniaxiale (à droite)
et évolution de la cohésion d déduite des données expérimentales (à gauche).
(
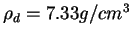 )
)
|
|
Pour le mécanisme associé à la surface du Cap, il est possible de
déterminer les paramètres (R et  ) par l'intermédiaire des
mesures issues d'un dispositif de compression triaxiale de
révolution. Le résultat du calage des paramètres R et
) par l'intermédiaire des
mesures issues d'un dispositif de compression triaxiale de
révolution. Le résultat du calage des paramètres R et  est
défini par les deux évolutions portées à la figure 6.2.4.
est
défini par les deux évolutions portées à la figure 6.2.4.
Figure 6.2.4:
Calage de la surface de charge (iso-densité) dans un plan
p-q à partir d'essais de compression triaxiale normalement
consolidés
|
|
Les évolutions quantitatives de R et  sont déterminées par
la méthode des moindres carrés appliquée sur l'ensemble des points
expérimentaux disponibles. La pression de consolidation
sont déterminées par
la méthode des moindres carrés appliquée sur l'ensemble des points
expérimentaux disponibles. La pression de consolidation  évolue avec la densité, elle-même liée à la déformation volumique
plastique et à la valeur de la densité initiale. Comme
évolue avec la densité, elle-même liée à la déformation volumique
plastique et à la valeur de la densité initiale. Comme  , les
trois paramètres (R, d,
, les
trois paramètres (R, d,  ) évoluent en fonction de la
déformation volumique plastique (voir figure 6.2.5).
) évoluent en fonction de la
déformation volumique plastique (voir figure 6.2.5).
Figure 6.2.5:
Évolution des paramètres de la surface de charge en
fonction de la déformation volumique plastique
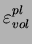 pour une masse volumique initiale de
pour une masse volumique initiale de
 .
(a)cohésion d (b) angle de frottement
interne
.
(a)cohésion d (b) angle de frottement
interne  (c) excentricité R (d) pression isotrope
(écrouissage)
(c) excentricité R (d) pression isotrope
(écrouissage) 
|
|
Les équations de ces évolutions sont les suivantes :
avec
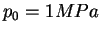
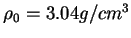 ,
,
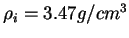 ,
,
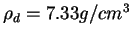 ,
,
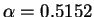 et
et
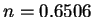 .
Le calage numérique de la surface du Cap à partir des mesures
issues du dispositif de compression triaxiale de révolution est
utilisé uniquement pour la simulation des pièces mises en forme au
sein de l'entreprise Federal Mogul dont la poudre présente un taux
de cire de 1%.
Les paramètres du mécanisme associés à la surface du Cap peuvent
être également déterminés par les mesures issues d'un dispositif
de compression en matrice. Moyennant quelques hypothèses
nécessaires au dépouillement des résultats expérimentaux, il est
possible de déterminer l'évolution des paramètres R et
.
Le calage numérique de la surface du Cap à partir des mesures
issues du dispositif de compression triaxiale de révolution est
utilisé uniquement pour la simulation des pièces mises en forme au
sein de l'entreprise Federal Mogul dont la poudre présente un taux
de cire de 1%.
Les paramètres du mécanisme associés à la surface du Cap peuvent
être également déterminés par les mesures issues d'un dispositif
de compression en matrice. Moyennant quelques hypothèses
nécessaires au dépouillement des résultats expérimentaux, il est
possible de déterminer l'évolution des paramètres R et  au
cours de la compression. Ces hypothèses permettent d'extraire des
résultats bruts le comportement de la poudre sans introduire les
effets dus au frottement avec l'outillage. L'essai de compression
en matrices se caractérise par des déformations radiales nulles ce
qui détermine dans le plan P-Q une direction particulière de pente
2/3 pour le vecteur écoulement. Par ailleurs, la surface du Cap
correspond à un modèle associé qui respecte la règle de normalité.
Le chemin de chargement lié à l'essai de compression en matrice
définit ainsi dans le plan P-Q le lieu des normales de pente 2/3
au cours de l'écrouissage par densification de la poudre (voir
figure 6.2.6).
au
cours de la compression. Ces hypothèses permettent d'extraire des
résultats bruts le comportement de la poudre sans introduire les
effets dus au frottement avec l'outillage. L'essai de compression
en matrices se caractérise par des déformations radiales nulles ce
qui détermine dans le plan P-Q une direction particulière de pente
2/3 pour le vecteur écoulement. Par ailleurs, la surface du Cap
correspond à un modèle associé qui respecte la règle de normalité.
Le chemin de chargement lié à l'essai de compression en matrice
définit ainsi dans le plan P-Q le lieu des normales de pente 2/3
au cours de l'écrouissage par densification de la poudre (voir
figure 6.2.6).
Figure 6.2.6:
Calage de la surface du Cap en fonction de la densité au
point d'intersection avec le chemin de chargement (normale à la
surface de pente 2/3)
|
|
À l'occasion de la campagne d'essais menée par la société Dorst,
trois centres de recherches ont fourni des mesures représentatives
de la compression en matrice. Une analyse détaillée de ces
résultats expérimentaux a été proposée au chapitre
2. Les trois chemins de contrainte dans le plan P-Q
au cours de la densification sont exposés par la figure
6.2.7.
Figure 6.2.7:
Chemin de contrainte dans un plan P-Q pour les trois
centres de recherches
|
|
Chaque chemin de contrainte donne lieu à la détermination de deux
évolutions quantitatives particulières de l'excentricité (R) et de
la pression de consolidation ( ). Pour les figures
6.2.8 et 6.2.9, les évolutions de ces deux
paramètres sont exprimées en fonction de la masse volumique.
). Pour les figures
6.2.8 et 6.2.9, les évolutions de ces deux
paramètres sont exprimées en fonction de la masse volumique.
Figure 6.2.8:
Évolution de l'excentricité du cap 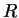 en fonction
de la masse volumique
en fonction
de la masse volumique
|
|
Figure 6.2.9:
Évolution de la pression de consolidation  en
fonction de la masse volumique
en
fonction de la masse volumique
|
|
Les courbes expérimentales ont été modélisées par des fonctions
mathématiques dont les extrapolations tiennent compte de certaines
hypothèses en rapport avec le comportement mécanique. À ce titre,
il est supposé nécessaire d'imposer un état de contrainte "infini"
en compression pour former un matériau sans aucune porosité. Le
comportement du matériau a pour limite la surface de de charge de
Von Mises lorsque la densité relative tend vers 1. Ainsi,
l'excentricité R a une asymptote verticale. Une asymptote
verticale est également associée à l'évolution de la pression de
consolidation  pour les fortes densités. La valeur de la
pression de consolidation est de l'ordre de 1 MPa lorsque la
poudre est sans cohésion. Par ailleurs, l'augmentation du
paramètre
pour les fortes densités. La valeur de la
pression de consolidation est de l'ordre de 1 MPa lorsque la
poudre est sans cohésion. Par ailleurs, l'augmentation du
paramètre  est très faible aux premiers stades de la
compression du matériau à l'état pulvérulent. L'évolution de
est très faible aux premiers stades de la
compression du matériau à l'état pulvérulent. L'évolution de  est alors associée à une asymptote horizontale pour les très
faibles densités dont la valeur minimum correspond à la densité
apparente.
Les calages numériques de la surface du Cap à partir des données
issues de la compression en matrice sont utilisés uniquement pour
simuler la mise en forme de la pièce en H. Les évolutions de ces
paramètres sont, pour cette poudre à 0.6% de cire :
où
est alors associée à une asymptote horizontale pour les très
faibles densités dont la valeur minimum correspond à la densité
apparente.
Les calages numériques de la surface du Cap à partir des données
issues de la compression en matrice sont utilisés uniquement pour
simuler la mise en forme de la pièce en H. Les évolutions de ces
paramètres sont, pour cette poudre à 0.6% de cire :
où
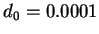 ,
,
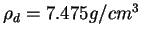 et
et
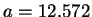 .
où
.
où
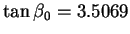 ,
,
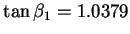 et
et
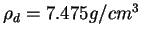 .
.
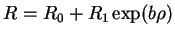 |
(6.39.1) |
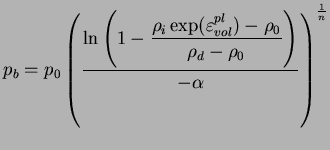 |
(6.39.2) |
Pour les évolutions données par les équations (6.2.1)
et(6.2.2) les coefficients sont donnés dans le tableau
suivant.
| |
3S |
Leicester |
AEA |
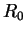 |
0.6174 |
0.5768 |
0.4640 |
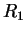 |
0.0003030 |
0.001311 |
0.002563 |
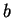 |
1.0006517 |
0.841932 |
0.851788 |
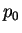 (MPa) (MPa) |
1 |
1 |
1 |
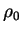 ( (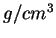 ) ) |
3.47 |
3.47 |
3.47 |
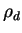 ( (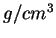 ) ) |
7.475 |
7.475 |
7.475 |
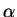 |
0.03539 |
0.6935 |
0.03259 |
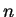 |
0.7009 |
0.6051 |
0.6930 |




suivant: Les paramètres du modèle
monter: Identification du comportement de
précédent: Les paramètres élastiques
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=6cm]{calaDP.eps}](img767.png)
![\includegraphics[width=6cm]{calaDP.eps}](img767.png)
![\includegraphics[width=16cm]{dbDorst.eps}](img768.png)
![\includegraphics[width=16cm]{calDPC.eps}](img769.png)
![\includegraphics[width=16.cm]{dbRPb.eps}](img770.png)

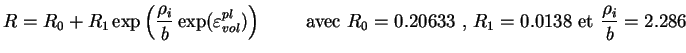
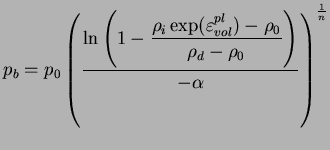
![\includegraphics[width=7cm,height=3.3cm]{calaCAP.eps}](img779.png)