suivant: Modèles plastiques anisotropes
monter: Modèles plastiques isotropes
précédent: Modèle modifié cohésif
Table des matières
Le modèle de Drucker-Prager/Cap
Ce modèle ayant été largement présenté par Pavier [PAV98],
cette partie ne présentera que le modèle tel qu'il est utilisé
dans le code de calcul Abaqus [HKS98a]. Sous cette forme, ce
modèle se décompose en deux surfaces. Une première surface de
rupture non-associée et une deuxième surface de cap associée comme
indiqué sur la figure 4.4.5 ou la figure 4.4.6.
Figure 4.4.5:
Représentation des surfaces de charges pour le modèle de Drucker-Prager/Cap
dans le plan des contraintes isotropes (p) contraintes déviatoires (q)
|
|
Figure 4.4.6:
Représentation des surfaces de charge pour le modèle de Drucker-Prager/Cap
dans l'espace des contraintes principales
|
|
Il y a une région de transition entre les mécanismes principaux de
manière à introduire une continuité entre les surfaces (pas de
point singulier). Les surfaces de charges sont les suivantes.
- La surface de rupture de Drucker-Prager dont l'équation
s'écrit :
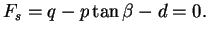 |
(4.28.6) |
Ce mécanisme est parfaitement plastique (pas d'écrouissage).
- La surface de charges du Cap d'équation :
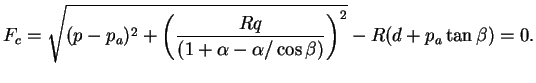 |
(4.28.7) |
Ce mécanisme est écrouissable.
- La surface de transition a pour équation :
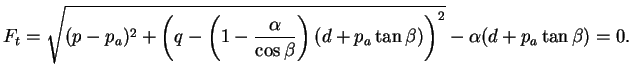 |
(4.28.8) |
Ce mécanisme est similaire à la surface de Drucker-Prager, il est
parfaitement plastique.
L'écrouissage est donné par une évolution de la variable  en
fonction de la déformation volumique plastique
en
fonction de la déformation volumique plastique
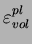 . Or, c'est le paramètre
. Or, c'est le paramètre 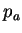 qui intervient dans les
équations (4.4.7) et (4.4.8). La relation qui lie la
variable
qui intervient dans les
équations (4.4.7) et (4.4.8). La relation qui lie la
variable 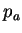 et la variable
et la variable  est la suivante :
Les écoulements plastiques sont définis par les potentiels
plastiques. Le potentiel associé aux surfaces de charge de
Drucker-Prager et de transition est commun et est :
est la suivante :
Les écoulements plastiques sont définis par les potentiels
plastiques. Le potentiel associé aux surfaces de charge de
Drucker-Prager et de transition est commun et est :
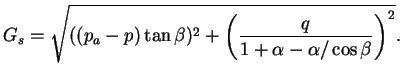 |
(4.28.9) |
Le potentiel associé à la surface de charges du Cap est donné par
:
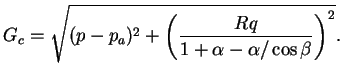 |
(4.28.10) |
Il est a noter que ces potentiels forment une surface de potentiel
continue comme l'indique la figure 4.4.7.
Figure 4.4.7:
Représentation des potentiels d'écoulement dans un plan p-q
|
|
Tel qu'il vient d'être présenté, le modèle ne peut qu'être
durcissant. Dans aucun cas, celui-ci ne peut présenter de
l'adoucissement étant donné que la surface de Drucker-Prager est
parfaitement plastique.
Le durcissement est donné par la surface écrouissable du Cap.
Étant donné un état de contraintes qui atteint la surface du
Cap, si celui-ci tend à croître, la déformation volumique
plastique augmente et par là même, modifie la position du Cap. Par
contre, si l'état de contraintes tend à diminuer, le comportement
est élastique.
La loi d'écrouissage est donnée par une relation entre la
déformation volumique plastique (
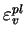 ) et le
paramètre
) et le
paramètre  . Cette relation est fonction du matériau étudié.
. Cette relation est fonction du matériau étudié.




suivant: Modèles plastiques anisotropes
monter: Modèles plastiques isotropes
précédent: Modèle modifié cohésif
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=10cm]{surfcap.eps}](img516.png)
![\includegraphics[width=10cm]{surfcap.eps}](img516.png)
![\includegraphics[width=10cm]{3dcap.eps}](img517.png)