



suivant: Le modèle de Drucker-Prager/Cap
monter: Les modèles de CamClay
précédent: Modèle modifié non-cohésif
Table des matières
Afin de prendre en compte la cohésion qui apparaît notamment dans
le cas des poudres métalliques, le modèle précédent a été enrichi
d'une cohésion isotrope 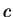 . Cette cohésion correspond à la limite
de résistance en traction isotrope. La surface de charges de ce
modèle est donnée par l'équation (4.4.5).
. Cette cohésion correspond à la limite
de résistance en traction isotrope. La surface de charges de ce
modèle est donnée par l'équation (4.4.5).
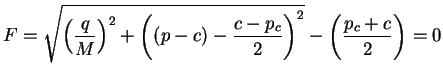 |
(4.28.5) |
Ce modèle étant associé, le potentiel est confondu avec la surface
de charge. Cette surface de charges peut être soit représentée
dans l'espace des contraintes principales (figure 4.4.3)
soit dans le plan p-q (contrainte isotrope-contrainte déviatoire)
présenté figure 4.4.4.
Figure 4.4.3:
Représentation du critère de CamClay dans l'espace des contraintes
principales
|
|
Figure 4.4.4:
Représentation du critère de CamClay dans le plan contrainte
isotrope(p)- contrainte déviatoire (q)
|
Cette figure permet d'expliquer plus facilement le fonctionnement
de ce modèle. Ce fonctionnement est identique aux deux premiers
modèles présentés.
C'est ce dernier modèle qui a été intégré dans le code de calcul
éléments finis Abaqus.




suivant: Le modèle de Drucker-Prager/Cap
monter: Les modèles de CamClay
précédent: Modèle modifié non-cohésif
Table des matières
FRACHON Arnaud
2002-11-12
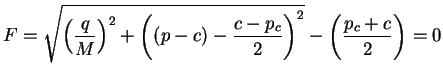
![\includegraphics[width=9.5cm]{2dcmcl.eps}](img515.png)