



suivant: Simulations des pièces Federal
monter: Identification du comportement de
précédent: Les paramètres de Drucker-Prager/Cap
Table des matières
Le modèle de CamClay mis en  uvre correspond à une version
modifiée avec cohésion. Cette cohésion
uvre correspond à une version
modifiée avec cohésion. Cette cohésion 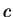 est posée constante et
égale à 1 MPa. Les évolutions numériques des paramètres M et
est posée constante et
égale à 1 MPa. Les évolutions numériques des paramètres M et 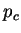 ont été déterminées à partir des mesures issues du dispositif de
compression en matrices. Les évolutions de ces paramètres sont
illustrées par les figures 6.2.10 et 6.2.11, les
données expérimentales correspondent à l'essai de compression en
matrices réalisé au laboratoire 3S.
ont été déterminées à partir des mesures issues du dispositif de
compression en matrices. Les évolutions de ces paramètres sont
illustrées par les figures 6.2.10 et 6.2.11, les
données expérimentales correspondent à l'essai de compression en
matrices réalisé au laboratoire 3S.
Figure 6.2.10:
Evolution de la pente d'état critique M en
fonction de la densité
|
|
Figure 6.2.11:
Evolution de la pression de consolidation 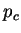 en
fonction de la densité
en
fonction de la densité
|
|
Ces paramètres sont décrit par les équations d'évolutions
suivantes :
avec

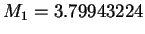 ,
,
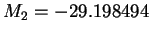 et
et
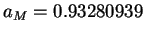 ,
avec
,
avec
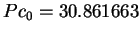 ,
,
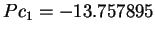 ,
,
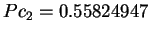 ,
,
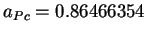 et
et
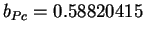 .
Les évolutions de ces paramètres permettent finalement de décrire
dans le plan P-Q les surfaces de charge en fonction de la masse
volumique de la poudre ainsi que l'illustre la figure
6.2.12.
.
Les évolutions de ces paramètres permettent finalement de décrire
dans le plan P-Q les surfaces de charge en fonction de la masse
volumique de la poudre ainsi que l'illustre la figure
6.2.12.
Figure 6.2.12:
Faisceau d'iso-masse volumique pour les surfaces de
charge du modèle de CamClay
|
|
Les techniques et hypothèses de calage évoquées pour le modèle de
Drucker-Prager/Cap ont été réutilisées pour définir les
évolutions de M et 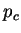 . Ces deux évolutions et le modèle
CamClay sont utilisés pour toutes les simulations du procédé
ayant recours à ce modèle.
. Ces deux évolutions et le modèle
CamClay sont utilisés pour toutes les simulations du procédé
ayant recours à ce modèle.




suivant: Simulations des pièces Federal
monter: Identification du comportement de
précédent: Les paramètres de Drucker-Prager/Cap
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=12.5cm]{M(rho).eps}](img795.png)