Modèle éléments finis 4

La dernière modélisation de la mise en forme de la pièce B est menée en modélisant les outils par des éléments finis au comportement élastique. Le matériau constitutif des outils se caractérise par un module d'Young de 210 GPa et un coefficient de Poisson de 0.3. Les dimensions des outils sont données sur la figure 6.3.18 . Le comportement de la poudre est régi par le modèle de Drucker-Prager/Cap. La répartition de densité suite à l'éjection est illustrée sur la figure 6.3.19.

Figure 6.3.18: Dimensions des outils élastiques intégrés à la simulation numérique. Module d'Young 210 GPa et coefficient de Poisson 0.3

Figure: Résultats de la répartition de masse volumique dans la pièce B pour les conditions de simulation n^&cir#circ;4, suite à l'éjection

Tableau 6.3.11: Résultats de la comparaison entre les mesures expérimentales et la simulation numérique sur les masses volumiques pour la pièce B, pour les conditions de simulation 4

masse volumique en 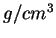$g/cm^3$	zone 1	zone 2	zone 3	zone 4	zone 5	dispersion
mesures	6.85	6.90	7.01	6.92	6.98
simulation en fin de compression	6.76	6.80	6.96	6.92	6.92
différence relative (%)	1.34	1.54	0.77	-0.03	0.82	1.57
simulation suite à l'éjection	6.67	6.71	6.81	6.72	6.82
différence relative (%)	2.72	2.83	2.94	2.53	2.35	0.59

Le tableau 6.3.11 présente les résultats des répartitions de masse volumique en fin de compression et suite à l'éjection. Dans un cas comme dans l'autre, il s'avère que les masses volumiques sont inférieures aux mesures expérimentales. Les valeurs proposées au tableau 6.3.11 peuvent être comparées aux résultats des modèles n^&cir#circ;1 et n^&cir#circ;2 afin d'apprécier les effets dus à l'élasticité simulée pour l'outillage. Par ailleurs, les cinématiques introduites au modèle n^&cir#circ;4 sont identiques à celles déjà utilisées pour les modèles n^&cir#circ;1 et n^&cir#circ;2. Il est à noter que les déplacements imposés sont déclarés sur les bases des poinçons qui ne sont pas en contact avec la poudre. Sous l'action des contraintes simulées, les poinçons ainsi décrits sont soumis à des déformations axiales de compression. En fin de compression, les hauteurs associées à la pièce B sont supérieures au cas des modèles n^&cir#circ;1 et n^&cir#circ;2. Le volume simulé en fin de compression par le modèle n^&cir#circ;4 est supérieur au volume correspondant du modèle n^&cir#circ;1. Suite à la décharge et à l'éjection, le volume simulé par le modèle n^&cir#circ;4 est le volume le plus grand parmi les quatre simulations de la pièce B. Ces remarques expliquent que les valeurs de masse volumique simulées par le modèle n^&cir#circ;4 en fin de compression et en fin d'éjection sont toujours inférieures aux valeurs mesurées. L'effet de l'incertitude de mesure sur les déplacements expérimentaux joue ici encore un rôle important. Les répartitions de densité conservent un grand intérêt lorsque les différences relatives entre zones et les dispersions associées sont analysées. En fin de compression, la différence entre le maximum et le minimum des écarts relatifs est de 1.57% alors que suite à l'éjection cette amplitude de dispersion sur les différences relatives se réduit à 0.59%. L'écart de masse volumique entre les mesures et les valeurs simulées après éjection est très homogène et de l'ordre de 0.18$g/cm^3$. Une correction possible consistant à appliquer une réduction de volume arbitraire au volume final simulé a été évoquée lors de l'analyse des résultats du modèle n^&cir#circ;2. Ce type de correction permettrait également dans le cadre des résultats du modèle n^&cir#circ;4 d'obtenir des valeurs de masse volumique remarquablement proches des valeurs mesurées. La simulation de la phase d'éjection a donc permis de décrire une bonne distribution des masses volumiques (au sens des gradients). Cette conclusion rejoint ce qui a été observé à l'occasion des résultats associés au modèle n^&cir#circ;2 pour un cycle de compression-décharge-éjection avec des outils supposés rigides. Le tableau 6.3.12 présente la comparaison des efforts en fin de compression entre la mesure et la simulation numérique.

Tableau 6.3.12: Résultats de la comparaison entre les mesures expérimentales et la simulation numérique sur les efforts pour la pièce B, pour les conditions de simulation 4

forces en MN	poinçon supérieur	poinçon inférieur	poinçon inférieur
		extérieur	intérieur
mesures	-2.39	0.63	1.52
simulation	-1.93	0.587	1.01
différence relative (%)	24	7	50

Ce tableau indique que les efforts simulés sont tous inférieurs aux valeurs de mesure. Cette sous-estimation numérique coïncide avec les sous-estimations systématiques de la masse volumique. Le volume simulé en fin de compression est supérieur au volume réel car les hauteurs simulées sont supérieures de quelques dixièmes aux hauteurs réelles. Le paramètre $p_b$ du modèle de Drucker-Prager/Cap croit exponentiellement avec la densité relative dès lors que celle-ci est supérieure à 0.9. Cela signifie que les efforts axiaux sur les poinçons augmentent aussi exponentiellement lorsqu'il s'agit de poursuivre la densification à partir d'une valeur de l'ordre de 6.5$g/cm^3$. Les valeurs des différences relatives sur les efforts (tableau 6.3.12) traduisent finalement la grande sensibilité des efforts aux hauteurs simulées en fin de compression, ce qui est en première approximation dû à l'évolution adoptée pour $p_b$ en fonction de la densité relative. La figure 6.3.19 compare la mesure et les résultats de simulation relatifs au rebond élastique radial. Le rebond radial simulé est presque constant suivant la hauteur de la pièce. Ce résultat se distingue nettement de l'évolution présentée pour le modèle n^&cir#circ;2. L'écart maximum avec la mesure est de 0.0247mm soit une différence relative de 15%. Le comportement élastique des outils intégré au modèle du procédé a donc une influence significative sur le résultat du rebond radial simulé. L'état de contraintes dans la pièce suite à l'éjection est illustré par la figure 6.3.20 au travers des invariant p et q.

Figure 6.3.20: État de contraintes dans la pièce B pour le modèle éléments finis 4 : pression isotrope (à gauche) et contraintes équivalente de Von Mises (à droite)

Cette figure indique un état de contraintes résiduelles relativement faible sauf au coin intérieur. Par ailleurs, les pressions isotropes négatives combinées aux contraintes équivalentes de Von Mises sont susceptibles de révéler un état de ruine ainsi que cela a été observé pour le modèle éléments finis 2. En effet, le point commun à ces modèles est l'absence de contre-force lors de l'éjection. cependant, dans le cas présent, les outils au comportement élastique semble diminuer l'influence de la contre-force tant au niveau du rebond à l'éjection, sur les répartitions de masses volumiques que des contraintes dans le matériau.