



suivant: Les paramètres plastiques
monter: Sensibilité aux paramètres élastiques
précédent: Le module d'Young
Table des matières
La figure 7.6.2(A) indique une faible variation de la
répartition de densité, ceci même pour les fortes variations de
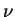 qui sont de l'ordre de 100%.
qui sont de l'ordre de 100%.
Figure 7.6.2:
Résultats de la sensibilité des répartitions de densités
et des efforts par rapport aux variations relatives du coefficient
de Poisson
|
|
L'influence des diverses valeurs du coefficient de Poisson sur les
écarts relatifs en densité est complexe. Il n'est pas possible de
trouver des évolutions monotones des écarts relatifs des sorties
en fonction de la croissance de 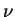 par exemple. La variation de
par exemple. La variation de
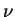 semble mettre en jeux, de manière parfois antagoniste sur
les effets, l'ensemble des mécanismes qui équilibre l'écoulement
de la poudre.
Les efforts en fin de compression sont fortement modifiés lorsque
le coefficient de Poisson atteint sa valeur maximum comme
l'illustre la figure 7.6.2(B). Cet aspect s'avère
surtout pour les fortes valeurs de
semble mettre en jeux, de manière parfois antagoniste sur
les effets, l'ensemble des mécanismes qui équilibre l'écoulement
de la poudre.
Les efforts en fin de compression sont fortement modifiés lorsque
le coefficient de Poisson atteint sa valeur maximum comme
l'illustre la figure 7.6.2(B). Cet aspect s'avère
surtout pour les fortes valeurs de 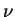 . L'influence de ce
paramètre élastique est certes complexe mais semble identique à
celle du module d'Young lorsque
. L'influence de ce
paramètre élastique est certes complexe mais semble identique à
celle du module d'Young lorsque 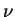 vaut 0.4. Le module
d'élasticité volumique K dépendant de
vaut 0.4. Le module
d'élasticité volumique K dépendant de 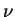 par la relation
(
par la relation
(
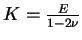 ). Ce module est ainsi maximisé par rapport
au cas de référence pour la valeur 0.4. La sensibilité de
). Ce module est ainsi maximisé par rapport
au cas de référence pour la valeur 0.4. La sensibilité de 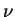 indique que ce paramètre est relativement important pour la
détermination des efforts sur les outils.
indique que ce paramètre est relativement important pour la
détermination des efforts sur les outils.




suivant: Les paramètres plastiques
monter: Sensibilité aux paramètres élastiques
précédent: Le module d'Young
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[height=8cm]{ressensNu.eps}](img896.png)
![\includegraphics[height=8cm]{ressensNu.eps}](img896.png)