



suivant: Le coefficient de Poisson
monter: Sensibilité aux paramètres élastiques
précédent: Sensibilité aux paramètres élastiques
Table des matières
La figure 7.6.1 illustre les influences des variations du
module d'Young pour les répartitions de densité et pour les
efforts.
Figure 7.6.1:
Résultats de la sensibilité des répartitions de densités
et des efforts par rapport aux variations relatives du module
d'Young au stade initial et au stade final
|
|
Les graphiques (A) et (C) traitent des influences pour les
densités par zone (A) et les efforts par poinçon (C) avec les
variations imposées sur les valeurs initiales au module d'Young.
De la même manière, les graphiques (B) et (D) concernent les
effets des variations imposées aux valeurs finales de E.
Le graphique 7.6.1 (A) indique que les variations
imposées à 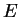 pour les faibles densités ont des effets très
limités et diffus sur les répartitions de densité en fin de
compression (-0.4% à +0.3%). Ces variations conduisent
à des fluctuations des efforts en fin de
compression sur un intervalle de -10% à +5% (figure 7.6.1(C)).
Les variations des
valeurs initiales du module d'Young modifient l'amplitude des
déformations nécessaires pour atteindre les états de contrainte
liés à la surface de charges initiale. L'activation du phénomène
de densification intervient en début de compression à des instants
légèrement décalés. L'histoire complète de la déformation jusqu'à
la fin du cycle de compression dissipe ces effets initiaux qui
sont alors limités.
Le graphique 7.6.1(B) montre que les valeurs de densité
sont graduellement décroissantes depuis une augmentation de la
densité dans la zone 5 vers une diminution dans la zone 1 lorsque
le module d'Young de référence est sous-estimé, et inversement.
Cela traduit une influence très légère du module d'Young sur
l'écoulement de la poudre lors de la compression (variation
relative de l'ordre de 0.3%). La sous-estimation de E traduit le
comportement d'un matériau "moins écrouis" pour une même densité
atteinte par rapport au cas de référence, l'écoulement de la
poudre est plus homogène dans le jupe. La surestimation de E
donne lieu à un comportement plus "rigide" qui augmente entre
autres les niveaux de contrainte dus aux frottements entre poudre
et outillage. Le commentaire suivant explicite cette remarque.
Les efforts simulés sont globalement croissants lorsque le module
d'Young augmente (7.6.1(C) et (D)). L'influence du module
d'Young sur les forces de compression peut être interprétée au
sens de la décomposition de la déformation. La déformation totale
est constante pour toutes les simulations car la cinématique est
fixée. La partition de la déformation entre contributions
élastiques et plastiques est par contre variable en fonction de E.
L'impact de ces deux contributions sur les résultats peut être
explicité pour un exemple de variation, le raisonnement restant
valide pour l'ensemble des effets observés à la figure
7.6.1. Une sous-estimation de E implique une
sous-estimation du module d'élasticité volumique K caractéristique
du massif de poudre. En considérant un état de contrainte
identique entre deux simulations pour un instant fixé du cycle de
compression, il vient que la simulation définit pour cet instant
un incrément de déformation volumique élastique plus grand et un
incrément de déformation volumique plastique plus petit par
rapport au cas de référence. Cette diminution de déformation
volumique plastique entraîne l'association à une surface de
charges dont la valeur de la consolidation
pour les faibles densités ont des effets très
limités et diffus sur les répartitions de densité en fin de
compression (-0.4% à +0.3%). Ces variations conduisent
à des fluctuations des efforts en fin de
compression sur un intervalle de -10% à +5% (figure 7.6.1(C)).
Les variations des
valeurs initiales du module d'Young modifient l'amplitude des
déformations nécessaires pour atteindre les états de contrainte
liés à la surface de charges initiale. L'activation du phénomène
de densification intervient en début de compression à des instants
légèrement décalés. L'histoire complète de la déformation jusqu'à
la fin du cycle de compression dissipe ces effets initiaux qui
sont alors limités.
Le graphique 7.6.1(B) montre que les valeurs de densité
sont graduellement décroissantes depuis une augmentation de la
densité dans la zone 5 vers une diminution dans la zone 1 lorsque
le module d'Young de référence est sous-estimé, et inversement.
Cela traduit une influence très légère du module d'Young sur
l'écoulement de la poudre lors de la compression (variation
relative de l'ordre de 0.3%). La sous-estimation de E traduit le
comportement d'un matériau "moins écrouis" pour une même densité
atteinte par rapport au cas de référence, l'écoulement de la
poudre est plus homogène dans le jupe. La surestimation de E
donne lieu à un comportement plus "rigide" qui augmente entre
autres les niveaux de contrainte dus aux frottements entre poudre
et outillage. Le commentaire suivant explicite cette remarque.
Les efforts simulés sont globalement croissants lorsque le module
d'Young augmente (7.6.1(C) et (D)). L'influence du module
d'Young sur les forces de compression peut être interprétée au
sens de la décomposition de la déformation. La déformation totale
est constante pour toutes les simulations car la cinématique est
fixée. La partition de la déformation entre contributions
élastiques et plastiques est par contre variable en fonction de E.
L'impact de ces deux contributions sur les résultats peut être
explicité pour un exemple de variation, le raisonnement restant
valide pour l'ensemble des effets observés à la figure
7.6.1. Une sous-estimation de E implique une
sous-estimation du module d'élasticité volumique K caractéristique
du massif de poudre. En considérant un état de contrainte
identique entre deux simulations pour un instant fixé du cycle de
compression, il vient que la simulation définit pour cet instant
un incrément de déformation volumique élastique plus grand et un
incrément de déformation volumique plastique plus petit par
rapport au cas de référence. Cette diminution de déformation
volumique plastique entraîne l'association à une surface de
charges dont la valeur de la consolidation  est inférieure au
cas de référence. Ainsi pour une cinématique fixée, l'état de
contrainte nécessaire à une densification permanente est de
moindre amplitude ce qui entraîne simultanément une diminution des
efforts simulés. Un raisonnement à état de contrainte identique
est en fait caduque, les effets observés sont la conséquence d'une
accumulation intégrale des contributions au cours de la procédure
numérique itérative de résolution.
Les graphiques 7.6.1(B) et (D) indiquent que les sorties
est inférieure au
cas de référence. Ainsi pour une cinématique fixée, l'état de
contrainte nécessaire à une densification permanente est de
moindre amplitude ce qui entraîne simultanément une diminution des
efforts simulés. Un raisonnement à état de contrainte identique
est en fait caduque, les effets observés sont la conséquence d'une
accumulation intégrale des contributions au cours de la procédure
numérique itérative de résolution.
Les graphiques 7.6.1(B) et (D) indiquent que les sorties
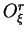 sont assez nettement perturbées, ce point étant en
rapport direct avec les amplitudes
sont assez nettement perturbées, ce point étant en
rapport direct avec les amplitudes
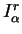 choisies pour les
valeurs finales du module d'Young E. Ainsi les écarts relatifs
maximaux sont de l'ordre de 1% pour les densités et surtout de
50% pour les efforts. Ces écarts relatifs sont calculés sur la
base des résultats de la simulation de référence.
Des écarts relatifs sont également présentés au chapitre
6, la valeur de référence utilisée ici étant
remplacée par la valeur expérimentale. Ce type de graphique permet
donc de manière indirecte d'anticiper sur des comparaisons entre
mesures expérimentales et résultats numériques. A titre d'exemple,
la valeur d'écart relatif de 50% associée au poinçon inférieur
intérieur (LIP) signifie que l'effort simulé (à partir d'une
diminution du module d'Young de référence) a varié d'un facteur 2
par rapport à l'effort simulé de référence. Cette amplitude de
variation peut être jugée trop grande dès lors qu'une comparaison
avec les valeurs expérimentales est envisagée. En effet, le
tableau 6.3.3 du chapitre 6 montre que le
cas de référence sous-estime de -14% l'effort mesuré sur le
poinçon inférieur intérieur. Cette sous-estimation est grandement
augmentée par la simulation qui intègre une diminution de la
valeur finale du module d'Young de référence. Ces commentaires
détaillés qui mettent en relation les chapitre 6 et
7 montrent les enjeux de l'étude de sensibilité
vis-à-vis de la prédictibilité des modèles numériques du procédé.
Ce type de commentaire n'est cependant pas reproduit par la suite.
La valeur du paramètre de sensibilité traduit en effet de manière
plus synthétique la dépendance et finalement la qualité des
résultats des simulations vis-à-vis de la précision des données
d'entrée.
choisies pour les
valeurs finales du module d'Young E. Ainsi les écarts relatifs
maximaux sont de l'ordre de 1% pour les densités et surtout de
50% pour les efforts. Ces écarts relatifs sont calculés sur la
base des résultats de la simulation de référence.
Des écarts relatifs sont également présentés au chapitre
6, la valeur de référence utilisée ici étant
remplacée par la valeur expérimentale. Ce type de graphique permet
donc de manière indirecte d'anticiper sur des comparaisons entre
mesures expérimentales et résultats numériques. A titre d'exemple,
la valeur d'écart relatif de 50% associée au poinçon inférieur
intérieur (LIP) signifie que l'effort simulé (à partir d'une
diminution du module d'Young de référence) a varié d'un facteur 2
par rapport à l'effort simulé de référence. Cette amplitude de
variation peut être jugée trop grande dès lors qu'une comparaison
avec les valeurs expérimentales est envisagée. En effet, le
tableau 6.3.3 du chapitre 6 montre que le
cas de référence sous-estime de -14% l'effort mesuré sur le
poinçon inférieur intérieur. Cette sous-estimation est grandement
augmentée par la simulation qui intègre une diminution de la
valeur finale du module d'Young de référence. Ces commentaires
détaillés qui mettent en relation les chapitre 6 et
7 montrent les enjeux de l'étude de sensibilité
vis-à-vis de la prédictibilité des modèles numériques du procédé.
Ce type de commentaire n'est cependant pas reproduit par la suite.
La valeur du paramètre de sensibilité traduit en effet de manière
plus synthétique la dépendance et finalement la qualité des
résultats des simulations vis-à-vis de la précision des données
d'entrée.




suivant: Le coefficient de Poisson
monter: Sensibilité aux paramètres élastiques
précédent: Sensibilité aux paramètres élastiques
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[height=9cm]{ressensE.eps}](img895.png)
![\includegraphics[height=9cm]{ressensE.eps}](img895.png)