



suivant: L'anisotropie plastique et effet
monter: Théorie plastique pour les
précédent: Rotation de l'espace des
Table des matières
Des argiles aux comportements anisotropes (sédimentation) ont été
étudiées par Gajo & al. [GW01]. Deux types
d'argiles ont ainsi été comparées : l'argile naturelle et l'argile
remaniée. Dans le cas de l'argile naturelle, un comportement
anisotrope est immédiatement détectable. Pour l'argile remaniée
initialement isotrope, l'anisotropie plastique est induite par
l'histoire de chargement.
Ces auteurs proposent de "normaliser" l'espace des contraintes
afin de représenter la limite élastique par une unique surface.
Plus précisément, l'espace décrit par les invariants est normé.
L'opération de normalisation de cet espace prend en compte trois
types d'écrouissages :
- l'écrouissage isotrope,
- l'écrouissage cinématique et
- l'écrouissage anisotrope dénommé
"écrouissage tournant".
La surface de charges est supposée posséder un centre (à
l'intérieur de la surface fermée convexe). Dans l'espace des
invariants des contraintes "réelles" (de Cauchy), l'état de
contrainte est donné par le vecteur de composantes 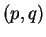 (voir
figure 4.5.7). La composante
(voir
figure 4.5.7). La composante 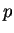 est donnée pour
une compression triaxiale de révolution comme le résultat de
l'addition de la contrainte axiale et de deux fois la contrainte
radiale, le tout étant divisé par -3. La composante
est donnée pour
une compression triaxiale de révolution comme le résultat de
l'addition de la contrainte axiale et de deux fois la contrainte
radiale, le tout étant divisé par -3. La composante 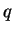 est la
différence entre la contrainte axiale et la contrainte radiale.
Des valeurs négatives de la composante
est la
différence entre la contrainte axiale et la contrainte radiale.
Des valeurs négatives de la composante 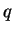 sont ainsi représentées
sur la figure 4.5.7.
sont ainsi représentées
sur la figure 4.5.7.
Figure 4.5.7:
L'espace des contraintes "réelles" (à gauche) est transformé
en un espace des contraintes "normalisées" (à droite)
|
|
Afin de centrer la surface à l'origine d'un espace de contrainte
modifiés, le tenseur
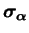 est retirer à
est retirer à
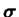 .
Cette première transformation est illustrée par la figure
4.5.8.
.
Cette première transformation est illustrée par la figure
4.5.8.
Figure 4.5.8:
Modification de l'espace des contraintes par la prise en compte de
l'écrouissage cinématique
|
|
Ainsi est pris en compte l'écrouissage cinématique. À la suite
de quoi, ce tenseur modifié
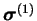 est divisé
par la contrainte isotrope
est divisé
par la contrainte isotrope 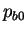 représentant l'écrouissage
isotrope.
Cette équation est illustrée par la figure 4.5.9.
représentant l'écrouissage
isotrope.
Cette équation est illustrée par la figure 4.5.9.
Figure 4.5.9:
Modification de l'espace des contraintes par la prise en compte de
l'écrouissage isotrope
|
|
Enfin, une rotation apparente est effectuée sur la surface ainsi
que le donne l'équation (4.5.16) par une diminution des
composantes déviatoires de l'espace des contraintes par un tenseur
déviatoire
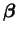 . Cette dernière opération permet de
prendre en compte l'écrouissage tournant.
. Cette dernière opération permet de
prendre en compte l'écrouissage tournant.
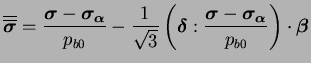 |
(4.29.16) |
où
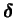 et le tenseur unité d'ordre deux. Cette
équation est illustrée par la figure 4.5.10.
et le tenseur unité d'ordre deux. Cette
équation est illustrée par la figure 4.5.10.
Figure 4.5.10:
Modification de l'espace des contraintes par la prise en compte de
l'écrouissage tournant
|
|
Il est alors intéressant de connaître l'évolution de ces
écrouissages et notamment, l'écrouissage tournant qui donne
l'évolution de l'anisotropie au cours de la compression d'argiles
remaniées. Ces différents écrouissages sont fonctions du tenseur
des vitesses de déformations plastiques
(
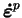 ) donné par la loi
d'écoulement (4.5.17).
) donné par la loi
d'écoulement (4.5.17).
![$\displaystyle \boldsymbol{\dot{\varepsilon}}^p = \frac{1}{H} [\boldsymbol{m} \o...
...{\overline{\boldsymbol{n}}}] : \dot{\overline{\overline{\boldsymbol
\sigma}}},$](img617.png) |
(4.29.17) |
où
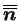 est la normale unitaire
à la surface de charges,
est la normale unitaire
à la surface de charges,
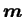 est la direction
d'écoulement plastique dans l'espace réel des contraintes et
est la direction
d'écoulement plastique dans l'espace réel des contraintes et 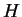 et le module plastique. Les écrouissages sont ainsi donnés par les
relations suivantes :
et le module plastique. Les écrouissages sont ainsi donnés par les
relations suivantes :
- écrouissage isotrope
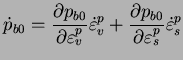 |
(4.29.18) |
où
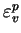 est la déformation volumique plastique et
est la déformation volumique plastique et
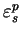 est la déformation déviatoire plastique
est la déformation déviatoire plastique
- écrouissage cinématique
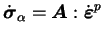 |
(4.29.19) |
où
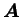 est une tenseur d'ordre quatre
est une tenseur d'ordre quatre
- écrouissage tournant
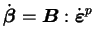 |
(4.29.20) |
où
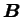 est un tenseur d'ordre quatre.
est un tenseur d'ordre quatre.
La fonction 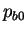 de l'équation (4.5.18), les tenseurs
de l'équation (4.5.18), les tenseurs
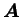 et
et
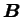 des équations (4.5.19)
et (4.5.20) respectivement ne peuvent être déterminées que
par l'expérience et l'observation des résultats de celles-ci.
Ainsi, les auteurs Gajo & al. [GW01] ont considéré
deux applications :
des équations (4.5.19)
et (4.5.20) respectivement ne peuvent être déterminées que
par l'expérience et l'observation des résultats de celles-ci.
Ainsi, les auteurs Gajo & al. [GW01] ont considéré
deux applications :
- argile naturelle dont l'anisotropie est inhérente
- argile remaniée qui est isotrope avant sollicitation.
La surface de charges dans l'espace normé est donnée par
l'équation (4.5.21).
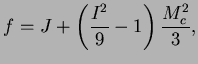 |
(4.29.21) |
où 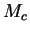 est la pente de la droite d'état critique,
est la pente de la droite d'état critique, 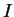 est la
contrainte moyenne et
est la
contrainte moyenne et 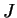 est la contrainte déviatoire de l'espace
normé.
Ici, nous ne nous intéresserons qu'à la deuxième application, car
c'est pour celle-ci que l'anisotropie est induite et se rapproche
le plus de ce qui se passe pour les poudres de fer.
L'anisotropie d'un sol remanié croît sous l'application d'un
chargement déviatoire. Afin d'analyser la rotation de la surface
dans l'espace réel des contraintes, il est supposé que
l'anisotropie induite est principalement pilotée par les
incréments de déformations plastiques déviatoires. Pour les états
critiques, de grandes déformations ne permettent pas d'induire une
anisotropie puisque le sol est constamment remanié. Ainsi,
l'évolution de l'anisotropie doit tenir compte de la distance à
l'état critique au travers d'une variable noté
est la contrainte déviatoire de l'espace
normé.
Ici, nous ne nous intéresserons qu'à la deuxième application, car
c'est pour celle-ci que l'anisotropie est induite et se rapproche
le plus de ce qui se passe pour les poudres de fer.
L'anisotropie d'un sol remanié croît sous l'application d'un
chargement déviatoire. Afin d'analyser la rotation de la surface
dans l'espace réel des contraintes, il est supposé que
l'anisotropie induite est principalement pilotée par les
incréments de déformations plastiques déviatoires. Pour les états
critiques, de grandes déformations ne permettent pas d'induire une
anisotropie puisque le sol est constamment remanié. Ainsi,
l'évolution de l'anisotropie doit tenir compte de la distance à
l'état critique au travers d'une variable noté 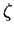 .
L'induction de l'anisotropie donne donc une évolution du tenseur
.
L'induction de l'anisotropie donne donc une évolution du tenseur
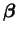 qui croît depuis zéro pour un état de
contrainte isotrope mais décroît vers zéro si l'état de
contraintes se rapproche de l'état critique. Une loi d'évolution
est alors proposée pour le tenseur
qui croît depuis zéro pour un état de
contrainte isotrope mais décroît vers zéro si l'état de
contraintes se rapproche de l'état critique. Une loi d'évolution
est alors proposée pour le tenseur
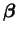 au travers
de l'équation (4.5.22).
au travers
de l'équation (4.5.22).
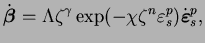 |
(4.29.22) |
ou 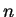 ,
, 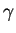 et
et 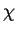 sont des paramètres constitutifs,
sont des paramètres constitutifs,
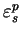 est l'amplitude de la déformation plastique
déviatoire courante et
est l'amplitude de la déformation plastique
déviatoire courante et 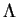 est une fonction matérielle
exprimé par l'équation (4.5.23).
est une fonction matérielle
exprimé par l'équation (4.5.23).
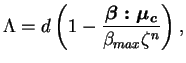 |
(4.29.23) |
où
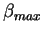 est un paramètre,
est un paramètre, 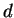 détermine le rapport pour
lequel
détermine le rapport pour
lequel
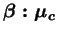 atteint la valeur de
saturation de
atteint la valeur de
saturation de
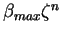 et
et
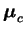 est la
direction unitaire de la composante déviatoire de la contrainte
(
est la
direction unitaire de la composante déviatoire de la contrainte
(
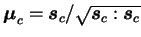 ).
Pour l'écrouissage cinématique, la proposition est donné par
l'équation (4.5.24).
).
Pour l'écrouissage cinématique, la proposition est donné par
l'équation (4.5.24).
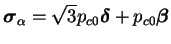 |
(4.29.24) |
La présence du tenseur
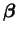 signifie la rotation
du grand axe de l'ellipse par rapport à l'axe des contraintes
isotropes. De plus, cette présence implique que l'évolution de
signifie la rotation
du grand axe de l'ellipse par rapport à l'axe des contraintes
isotropes. De plus, cette présence implique que l'évolution de
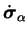 est fonction de
est fonction de
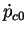 et de
et de
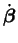 .
.




suivant: L'anisotropie plastique et effet
monter: Théorie plastique pour les
précédent: Rotation de l'espace des
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[height=5cm]{normalized_p-q.eps}](img604.png)
![\includegraphics[height=5cm]{normalized_p-q.eps}](img604.png)
![\includegraphics[]{normcine.eps}](img607.png)
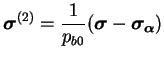
![\includegraphics[]{normiso.eps}](img611.png)
![\includegraphics[]{normaniso.eps}](img615.png)