L'anisotropie plastique et effet de trajet en métallurgie des poudres

En métallurgie des poudres, il est fréquent d'avoir la densité ou la déformation volumique plastique comme paramètre d'écrouissage. Ces paramètres sont particulièrement adaptés pour la description de l'écrouissage isotrope d'un modèle plastique isotrope associé ou non. De plus, la densité est un paramètre couramment utilisé pour décrire l'état du matériau au cours et en fin de compression. Cette indication est importante mais pas suffisante pour décrire l'état de déformation, bien que la majorité de l'état de déformations soit volumique. Il est également possible de rencontrer, plus rarement, le travail plastique pour ce paramètre. Dans sa thèse, Bonnefoy [BON01] utilise les iso-densités pour exprimer les surfaces de charges ainsi que l'illustre la figure 4.5.11.

Figure 4.5.11: Points d'iso-densités dans un espace des contraintes p-q pour différentes poudres résultant d'essais de compression triaxial

La similitude apparente des surfaces de charges l'a conduit à introduire les courbes maîtresses où l'état de contraintes est divisé par la pression de consolidation, ainsi qu'il est présenté sur la figure 4.5.12.

Figure 4.5.12: Points d'iso-densités dans un espace des contraintes (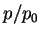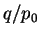$p/p_0$)-($q/p_0$) pour différentes poudres résultant d'essais de compression triaxial

Ce concept est à rapprocher de l'écrouissage isotrope dans la transformation de l'espace des contraintes de Gajo & al. [GW01]. Il est alors remarqué que ce concept est plus approprié pour les poudres d'alumine et de carbure de tungstène que pour les poudres de fer et de tungstène. Ces deux dernières poudres donnent à penser qu'une rotation de l'espace des contraintes permettrait d'obtenir une surface de charges unique pour le mécanisme de consolidation. Cette rotation, au sens de Gajo & al. [GW01], a pour signification un comportement plastique anisotrope. Ainsi, pour une compression triaxiale de révolution normalement consolidée, il y a un comportement plastique anisotrope induit. Rottmann & al. [RCR01] ont, quant à eux, mis en évidence, d'une part, le comportement plastique anisotrope d'un échantillon mis en forme par compression dométrique, et d'autre part, mis en évidence l'influence du chemin de sollicitation pour la mise en forme sur le comportement du matériau. De plus, lors de la caractérisation d'une poudre de fer, Pavier [PAV98] (pages 128-133) a, elle aussi, mise en relief l'importance du chemin de contrainte sur le comportement de la poudre lors de la compression (essais triaxial de révolution normalement consolidé et sur-consolidé). En outre, ce dernier auteur à également mis en évidence la non-associativité du mécanisme de consolidation. Ceci peut être alors modélisé par la proposition de Hueckel & al. [HT94] qui propose une rotation de la surface de charges mais pas du potentiel dans l'espace des contraintes. L'intersection de ces observations mène à considérer que le comportement plastique de la poudre de fer peut présenter un comportement anisotrope induit selon le mode de sollicitation mis en uvre. En outre, la transformation de l'espace des contraintes semble être une solution intéressante et pratique tant au niveau de la modélisation que pour l'intégration dans un code de calcul. En effet, cette méthode permet non seulement de traiter de l'anisotropie de la plasticité, mais également de celle de l'élasticité. Ainsi, en exprimant une loi élasto-plastique dans un espace des contraintes transformées, on obtient une loi élastique anisotrope et une loi plastique de même anisotropie. Cela implique une égalité de l'anisotropie entre l'élasticité et la plasticité. Cette égalité n'est pas toujours vérifiée, notamment pour le kaolin pour lequel Mitchell [MIT72] observe une anisotropie des déformations réversibles plus importante que celle des déformations permanentes. Seul, les résultats expérimentaux peuvent indiquer le degré d'anisotropie et l'évolution de celle-ci. Dans le cas de la poudre de fer, il est possible de proposer une transformation de l'espace des contraintes afin de prendre en compte l'écrouissage isotrope ($p_b$) et l'écrouissage anisotrope ( $\boldsymbol \beta$). 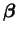Sans même avoir de résultats expérimentaux, il est possible de supposer que l'apparition de l'anisotropie est due à des sollicitations déviatoires et la disparition est due à des sollicitations isotropes ainsi que l'illustre la figure 4.5.13.

Figure 4.5.13: Évolution de la surface de charges selon que la sollicitation est déviatoire (à gauche) ou isotrope (à droite)

Le paramètre d'écrouissage qui permet de prendre en compte l'anisotropie plastique, peut être la déformation plastique (le tenseur complet), la contrainte appliquée (le tenseur complet aussi) ou encore un tenseur exprimant la distribution, l'amplitude et l'orientation des surfaces de contacts entre grains de poudres ainsi que le propose Oda & Ohnishi [OO92]. Cette liste ne se veut pas être exhaustive. Le paramètre d'écrouissage le plus adapté étant celui qui prend le mieux en compte l'essence des phénomènes, en l'occurrence, l'anisotropie.